
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практика 9. (8 дек 932025, 10 дек 932024)
Практика 9. (8 дек 932025, 10 дек 932024)
Задача 50. Найти 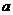 , при котором ранг равен 2.
, при котором ранг равен 2.
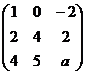
Решение. Преобразуем:
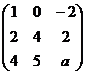

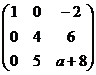

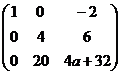

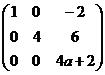
Последняя строка состоит из нулей при 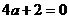 , т.е.
, т.е. 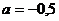 .
.
Ответ. 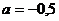 .
.
Задача 51. Найти 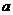 , при котором ранг равен 2.
, при котором ранг равен 2.
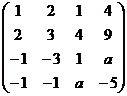
Решение.
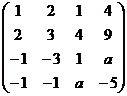
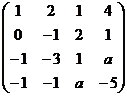

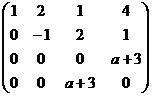 Ответ.
Ответ. 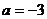 .
.
Глава 3.
Системы линейных алгебраических уравнений.
Задача 1.Решить систему линейных уравнений 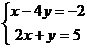 .
.
Решение. А. Матричным методом.
Запишем систему в виде: 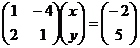 .
.
Найдём обратную матрицу для А.
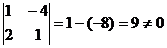 .
.
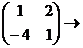
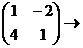
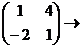

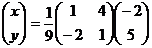 =
= 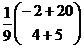 =
= 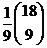 =
=  .
.
Б. Методом Крамера.
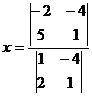 =
= 
 =
= 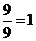 .
.
Ответ. 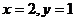 .
.
Метод Гаусса.
Задача 2. Решить систему уравнений 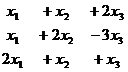
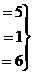
Решение.Построим расширенную матрицу и преобразуем её.

чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная 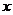 из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычесть удвоенную 1-ю.
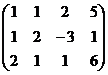

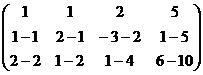 =
= 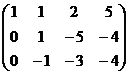
Теперь, чтобы обнулить ниже чем  , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
 =
= 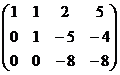
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
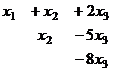
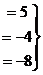 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 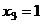 . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
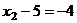
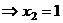 .
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда 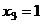 и
и 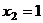 . Итак,
. Итак, 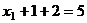
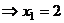 .
.
Ответ. 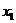 =2,
=2, 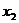 =1,
=1, 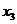 =1.
=1.
Можно ответ записать и в виде вектора: 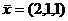 .
.
Ответ. 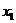 =2,
=2, 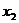 =1,
=1, 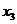 =1.
=1.
Задача 3. Решить систему уравнений 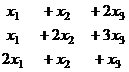
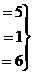
(как в прошлой, но у элемента 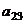 изменили знак).
изменили знак).
Решение.Построим расширенную матрицу и преобразуем её.
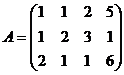
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная 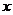 из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:
а) из 2-й строки вычесть 1-ю;
б) из 3-й строки вычесть удвоенную 1-ю.
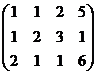

 =
= 
Теперь, чтобы обнулить ниже чем  , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
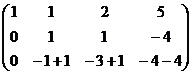 =
= 
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
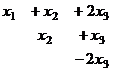
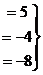 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить 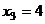 . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
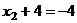
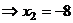 .
.
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, 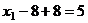
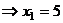 .
.
Ответ. 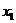 =5,
=5,  ,
, 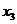 =4.
=4.
Можно ответ записать и в виде вектора:  .
.
Задача 4. Решить систему уравнений 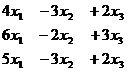
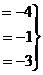
Решение. При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.
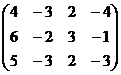

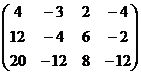

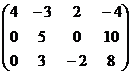

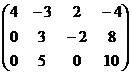
Чем ниже, тем меньше переменных. Идея метода Гаусса соблюдена.
Сначала можно найти х2, затем х3, позже х1.
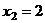 , тогда
, тогда 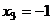 . Тогда
. Тогда 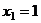 .
.
Замечание. Впрочем, в данном случае можно заметить, что совпадает существенная часть 1 и 3 строк, и если сразу вычесть 1-ю строку из 3-й, то можно будет тут же найти 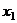 .
.
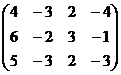

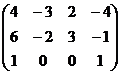
Из 3-го уравнения теперь следует 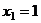 .
.
А далее можно составить более простую систему на 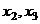 , уже с учётом
, уже с учётом 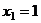 .
.
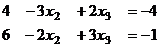
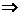
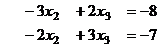
Теперь домножим, чтобы получить кратное, и приведём к треугольной структуре.
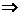
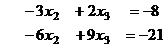
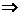
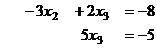
Из последнего 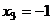 , а далее
, а далее 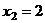 .
.
Ответ. 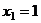 ,
, 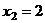 ,
, 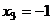 .
.
- - - Перерыв - - -
Задача 5. Решить систему уравнений 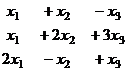

Решение. Составим расширенную матрицу.
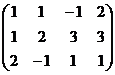

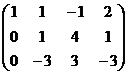

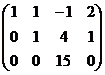
Получили эквивалентную систему:
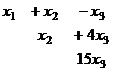
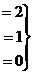 , из последнего уравнения, очевидно,
, из последнего уравнения, очевидно,  ,
,
тогда из предпоследнего 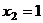 , и из 1-го
, и из 1-го 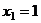 .
.
Ответ. 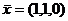 .
.
Задача 6. Решить систему уравнений 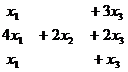
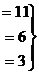
Решение.Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.
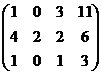



 =
=
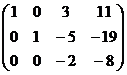 треугольная структура уже получилась.
треугольная структура уже получилась.
Перепишем снова в виде системы:
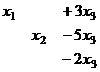
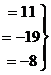 из 3-го уравнения
из 3-го уравнения 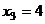 , подставляем во 2-е, там получается
, подставляем во 2-е, там получается 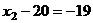
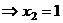 .
.
А из 1-го 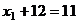
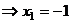 .
.
Ответ.  ,
, 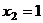 ,
, 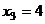 .
.
Задача 7. Решить систему уравнений 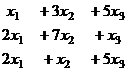
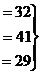
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|