
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практика 10. (9 дек 932025, 12 дек 932024)
Решение.
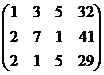

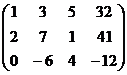



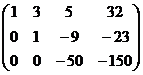


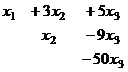

Из последнего, 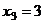 . Тогда из 2-го
. Тогда из 2-го 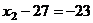 ,
, 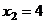 .
.
Тогда из 1-го 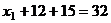 ,
, 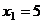 .
.
Ответ. (5,4,3).
Задача 8.Решить систему уравнений
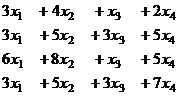
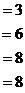
Решение.
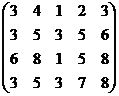

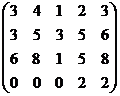


Система приведена к виду:
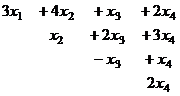

Из последнего, 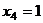 , тогда
, тогда 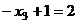
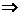
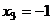 .
.
Тогда из 2-го: 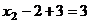 ,
, 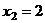 .
.
И наконец из 1-го, 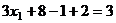
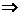

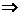
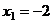 .
.
Ответ.  .
.
Задача 9.Решить систему уравнений
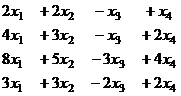

Решение. Здесь удобнее метод Гаусса начать с 4 столбца (зеркально), так как там коэффициенты, кратные 1.




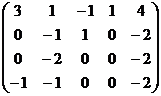
Из двух последних: 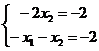
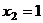 ,
, 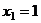 .
.
Тогда из первых двух уравнений:
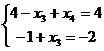
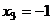 ,
, 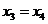 .
.
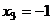 ,
, 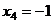 .
.
Ответ. 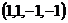 .
.
Практика 10. (9 дек 932025, 12 дек 932024)
Задача 10.Решить систему уравнений.
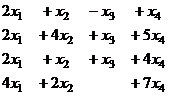

Решение.


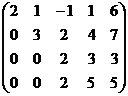

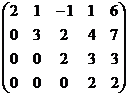
Разворачиваем обратно в систему:
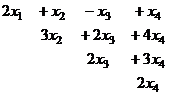
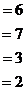
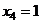
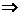
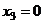
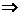
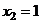
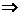
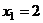 .
.
Ответ. 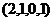 .
.
Неопределённые системы ( ).
Задача 11.Решить неоднородную систему 
Решение. 

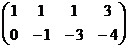

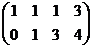 .
.


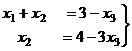 .
.
Из 1-го: 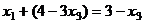 ,
, 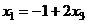
Ответ.Общее решение  .
.
Частные решения:  ,
, 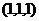 , ...
, ...
Для сравнения, методом Крамера.
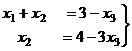
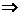
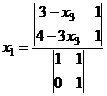 =
= 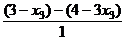 =
= 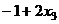 .
.
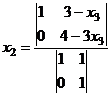 =
= 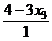 =
= 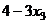 .
.
То же самое.
Задача 11-Б.Решить однородную систему 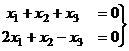
Решение. 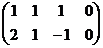

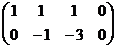

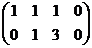 .
.


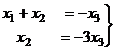 .
.
Из 1-го: 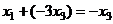 ,
, 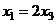
ФСР  . Обратите внимание, что это и есть разность двух частных решений прошлой задачи.
. Обратите внимание, что это и есть разность двух частных решений прошлой задачи.
Ответ.Общее решение  . ФСР
. ФСР  .
.
Задача 12.Решить неоднородную систему.
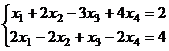
Решение.Построим и преобразуем расширенную матрицу.
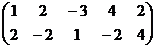

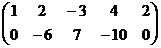
Базисный минор в первых двух столбцах, последние две переменные свободные, переносим их вправо.
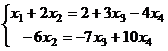
Отсюда 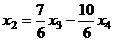 . Тогда
. Тогда 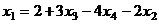 =
=
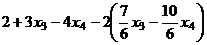 =
= 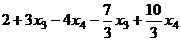 =
=
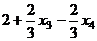 .
.
Ответ. Общее решение: 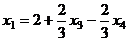 ,
, 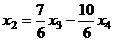 .
.
Частное например (2,0,0,0).
Задача 13.Решить неоднородную систему 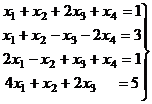
Решение.Запишем расширенную матрицу системы.

обнулим всё ниже углового элемента, для этого:
из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.
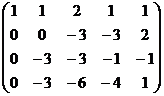
теперь можно поменять местами 2 и 3 строки, а также домножить на 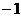 три последних уравнения (там почти везде были знаки минус)
три последних уравнения (там почти везде были знаки минус)
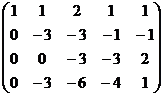


затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.


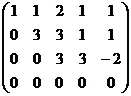
Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.
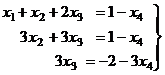
Из последнего уравнения  , подставляя это выражение во 2-е уравнение, выразим
, подставляя это выражение во 2-е уравнение, выразим 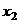 .
. 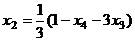 =
= 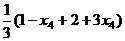 ,
,
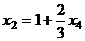 . Далее из 1-го уравнения:
. Далее из 1-го уравнения:
 =
=  ,
,
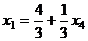 . Итак, общее решение:
. Итак, общее решение:
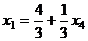 ,
, 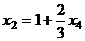 ,
,  .
.
Можно записать в виде вектора: 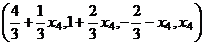 .
.
Если задать, например, 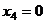 получим частное решение:
получим частное решение:  .
.
Ответ. Общее решение: 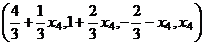 .
.
Задача 14.Решить неоднородную систему 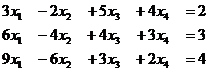
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|