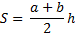JКак действовать

⇐ ПредыдущаяСтр 4 из 4

JКак действовать

Чтобы установить, что данный параллелограмм - ромб, докажите, что в нем:

ЛИБО 1) все стороны равны (определение ромба);

2) диагонали взаимно перпендикулярны (признак);

ТРАПЕЦИЯ

Определение Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие - непараллельны.

m – средняя линия

a, b – основания трапеции h – высота

Средняя линия трапеции – это отрезок, соединяющий середины её боковых сторон. Свойство средней линии трапеции: Средняя линия трапеции параллельна основаниям и равна их полусумме.

ПРЯМОУГОЛЬНАЯ ТРАПЕЦИЯ– трапеция, в которой одна из боковых сторон перпендикулярна основаниям (или один угол равен 90°)

Сумма градусных мер двух углов трапеции. Прилежащих к боквой стороне, равна 180°.

РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ– трапеция, в которой боковые стороны равны.

Свойство:

1) углы при основании равны;

2) диагонали равнобедренной трапеции равны.

3) диагонали образуют с ее основанием равные углы

Признак:

Если в трапеции углы при основании равны, то такая трапеция является равнобедренной.

Если боковая сторона трапеции равна меньшему основанию, то диагональ, соединяющая их концы, - биссектриса угла, прилежащего к большему основанию.

Если диагонали трапеции взаимно перпендикулярны, то средняя линия трапеции равна ее высоте.

Отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.

В равнобедренной трапеции сумма противолежащих углов равна 180°

Если в трапеции сумма противополжных углов равна 180°, то трапеция равнобедренная

JКак действовать

Если в условии задачи дана трапеция, то полезно такие дополнительные построения:

1)проведение высот(разбиваем трапецию на прямоугольник и прямоугольные треугольники)

2) проведение диагоналей(далее работаем с подобными треугольниками)

3) проведите через вершину трапеции прямую, параллельную боковой стороне, и используйте свойства полученных параллелограмма и треугольника.

⇐ Предыдущая 1 2 34