
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица V.8. Таблица V.9. Задача 3.4
Рис. V.30
Таблица V.8
| схема | 6 | 7 | 8 | 9 | а | ||||||
| столбец | |||||||||||
| F МН | 1.0 | 0.8 | 1.2 | 1.1 | 0.7 | 0.9 | 1.3 | 1.4 | 0.9 | 1.0 | б |
| l м | 1.5 | 1.6 | 1.7 | 1.5 | 1.8 | 2.0 | 1.2 | 0.9 | 1.3 | 1.2 | в |
| R МПа | б |


Рис. V.31
Таблица V.9
| схема | а | ||||||||||
| столбец | |||||||||||
| F кН | б | ||||||||||
| l м | 4.4 | 4.2 | 3.8 | 3.6 | 5.0 | 4.8 | 4.6 | 4.4 | 4.5 | в | |
| h см | а | ||||||||||
α 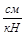
| б | ||||||||||
| № I | в |
Задача 3.4
На двутавровую балку (рис.V.32, а) с высоты h падает груз F. Требуется:
1) найти наибольшее нормальное напряжение в балке;
2) решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость которой α (осадка от груза 1 кН);
3)Сравнить полученные результаты.

| Исходные данные:
F = 30 кН; l = 2.4 м; h = 3 см; a = 4 двутавр № 24.
Вычисляя реакции опор RA = 24 кН, RB = 6 кН, (рис. V.32), построим эпюру изгиба- ющих моментов MF (рис. V.32, в).
Динамическое напряжение σd = χ d ·σст где:
Для определения прогиба балки в точке К при статическом приложе-нии силы F построим эпюру
|

| |
 Рис. V.32
Рис. V.32
| |
|
| |
Вычислим 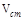 , перемножив эпюры
, перемножив эпюры  и
и 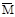 по способу Верещагина:
по способу Верещагина:

Момент инерции и момент сопротивления для двутавра №24 возьмем и из сортамента : Iz=3460 см4; Wz=289 см3. Модуль продольной упругости для стали Е=2·105 МПа:
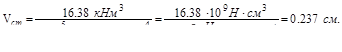
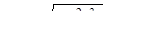
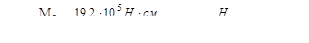
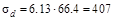 МПа.
МПа.
Если правую опору заменить пружиной, то за счет осадки пружины опо-ра В переместится на величину (рис. V.32, д):
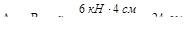 , а точка К, расположенная на
, а точка К, расположенная на 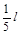 от не-подвижной опоры А переместится на:
от не-подвижной опоры А переместится на:

Полное перемещение точки К равно
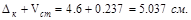
В этом случае
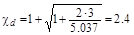 и
и 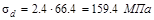 .
.
Сопоставляя первый и второй расчеты можно сделать вывод, что уста-новка податливой опоры снижает динамические напряжения в данном случае, более чем в 2.5 раза.
ПРИЛОЖЕНИЕ I
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|

 ;
;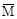 от единичной силы, приложенной в этой точке в направлении вектора F. (рис. V.32, г).
от единичной силы, приложенной в этой точке в направлении вектора F. (рис. V.32, г).