
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольное задание 3.. Задача 3.2
Контрольное задание 3.
Задача 3.1.Короткий чугунный стержень сжимается продольной силой F, приложенной в точке А. (рис.V.25). Требуется:
1) проверить условие прочности стержня, если допускаемые напряжения при сжатии 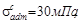 а при растяжении
а при растяжении 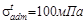
2) определить положение нейтральной оси и построить эпюру σ , приняв за базу перпендикуляр к нейтральной оси.
Пример решения:
Исходные данные: F = 200 кН; a = b = 4 см.
Поскольку в формулу для определения напряжений при внецентренном растяжении - сжатии 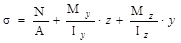 входят геометричес-кие характеристики сечения и координаты точек сечения в системе главныхцентральных осей инерции, то в первую очередь следует найти положение этих осей.
входят геометричес-кие характеристики сечения и координаты точек сечения в системе главныхцентральных осей инерции, то в первую очередь следует найти положение этих осей.
Сечение (рис. V.25) имеет горизонтальную ось симметрии zo, которая и является одной из главных центральных осей инерции.
Проведем ось y вертикально, так, чтобы все сечение располагалось спра-ва от нее. Представим сплошное сечение вертикальным прямоугольником пло-щадью А=4 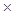 16=64 см2 и двумя горизонтальными, площадью А=12
16=64 см2 и двумя горизонтальными, площадью А=12 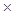 4 = 48 см2, каждый. Центры тяжести прямоугольников удалены от оси у на рассто-янии z = 2 и z =10 см, соответственно. Координата центра тяжести сложного се-чения:
4 = 48 см2, каждый. Центры тяжести прямоугольников удалены от оси у на рассто-янии z = 2 и z =10 см, соответственно. Координата центра тяжести сложного се-чения:
 ,
,
а общая площадь сечения (ΣAi) равна 160 см2.

Рис. V.25
Таким образом, определена другая главная центральная ось инерции yo, (см. рис.V.25). Моменты инерции сечения относительно этих осей:
где  - расстояния центров тяжести прямоугольников до осей yo и zo соответ-ственно.
- расстояния центров тяжести прямоугольников до осей yo и zo соответ-ственно.
Изгибающие моменты, входящие в формулу для определения напряже-ния, создаются сжимающей силой F = -200 кН, которая приложена в точке А с координатами 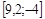 , тогда:
, тогда:
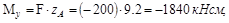 ;
;
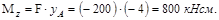
Наибольшие значения напряжений в растянутой и сжатой зонах можно вычислить, если известны координаты «опасных» точек. Эти точки наиболее удалённые от нейтральной оси, положение которой определяется отрезками уо, zo, отсекаемыми ею на осях координат. При этом:
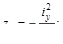
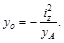
Квадраты радиусов инерции равны
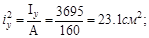

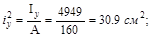

Итак, 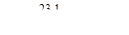
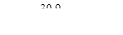
Проведя нейтральную ось (н.о. на рис. V.25), находим наиболее удален-ные от нее точки С (-6.8; 8) и Д (9.2; -8).
Определим напряжения в этих точках:
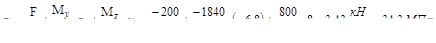
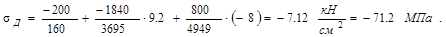
На перпендикулярах к базовой линии отложим в масштабе значения нап-ряжений для точек С и Д и, соединив эти точки прямой линией, построим эпю-ру σ. Используя эту эпюру легко определить напряжения в любой точке сече-ния. Для этого достаточно восстановить перпендикуляр к базовой линии из этой точки ( например из точки А), измерить отрезок nnи, зная масштаб построения эпюры, определить величину напряжения в точке.
Условие безопасной прочности в сжатой зоне 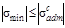 выполняется, т.к.
выполняется, т.к. 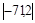 <
< 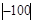 МПа, а условие прочности в растянутой зоне
МПа, а условие прочности в растянутой зоне 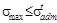 , не выполняется, т.к. 34.3 мПа больше допускаемого напряжения (30 МПа) и пере-грузка
, не выполняется, т.к. 34.3 мПа больше допускаемого напряжения (30 МПа) и пере-грузка 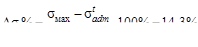 , не допустима.
, не допустима.
Исходные данные для задачи 3.1 приняты в соответствии с рис. V.26 и таблицей V.5, а для задачи 3.2 рис. V.27 и таблица V.6.
Задача 3.2
На стержень круглого поперечного сечения, расположенный в горизон-тальной плоскости и имеющий прямые углы в точках излома действует верти-кальная нагрузка в соответствии с изображением на рис. V.28, а).
Требуется:
1) построить отдельно (в аксонометрии) эпюры изгибающих и крутя-щих моментов;
2) установить опасные сечения, найти для них величины расчетного момента по четвертой теории прочности и диаметр стержня, приняв 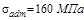
Исходные данные: F=3кН, q =  l=2м.
l=2м.
|



 Таблица V.5
Таблица V.5
| схема | а | ||||||||||
| столбец | |||||||||||
| n см k см | б | ||||||||||
| F кН | а | ||||||||||
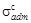
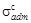
| б |



V.27
Таблица V.6
| Схема | а | ||||||||||
| столбец | |||||||||||
| F кН | б | ||||||||||
q 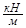
| а | ||||||||||
| l м | 1.5 | 2.5 | 3.5 | 1.5 | 2.5 | 3.5 | б | ||||
| σadm МПа | в |

Рис. V.28
Используя метод сечений, определим изгибающие и крутящие моменты на каждом участке (рис. V.28, а). Обозначим для каждого участка местную сис-тему координат с началом в центре тяжести сечения и осями, направленными по направлению главных осей инерции поперечного сечения: вдоль оси стерж-ня –x; перпендикулярно оси - y, z, образующие правую систему координат.
Участок I ( 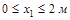 )
)
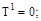
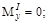
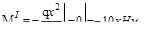
Участок II ( 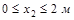 ).
).
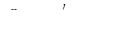 ;
; 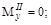
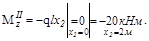
Участок III ( 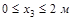 )
)
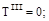
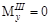 ;
; 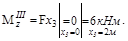
Участок IV ( 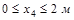 )
) 
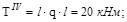
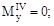

Эпюры Mz и Т даны на рис.V.28, б, в, г. Опасными могут быть сечение в заделке, где Mz=-18 кНм и Т=20 кНм.
Определяемый по четвертой теории прочности эквивалентный момент для круглого сечения 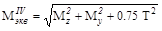
В заделке
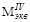
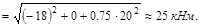
На втором участке стержня, где Mz= -20 кНм и Т= -10 кНм, имеем
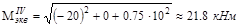 .
.
Анализируя расчеты, делаем вывод, что наиболее опасным является се-чение в заделке.
Определим диаметр стержня, при котором будет обеспечена безопасная прочность
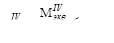
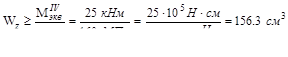 .
.
Для круга осевой момент сопротивления 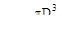 и он должен быть не менее 156.3 см3, тогда диаметр стержня
и он должен быть не менее 156.3 см3, тогда диаметр стержня
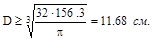 .
.
Задача 3.3
Для стойки (рис. V.29) указанного сечения, одинаково закрепленной в плоскостях xy и xz потери устойчивости и сжатой центрально приложенной силой F требуется подобрать размеры поперечного сечения, c использованием коэффициента продольного изгиба с нею. Материал - сталь Ст-3.

| Исходные данные:
F =1000 кН; l =1.5 м; R= 220 МПа.
Для стойки, имеющей защемляющую и шарнирную опоры, коэффициент приведенной длины μ = 0.7
Определим геометрические характеристики
сечения:
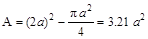 ; ;
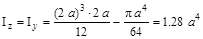 ; ;
|
Рис. V.29
радиусы инерции сечения
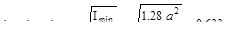
Гибкость стержня
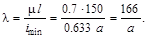
Коэффициент продольного изгиба может принимать значения от нуля, до единицы в первом приближении 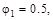 тогда:
тогда:
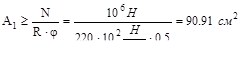 ;
;
 ;
; 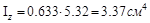 ;
;
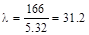 .
.
По табл. (приложение) принимаем значения 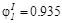 , которое сущес-твенно отличается от φ1.
, которое сущес-твенно отличается от φ1.
Во втором приближении коэффициент продольного изгиба принимаем как среднее арифметическое:
 .
.
Повторяем расчет во втором, третьем и четвертом приближении (табл. V.7)
Таблица V.7
| Приближение | 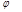
| 
| 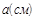
| 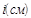
| 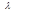
| j I |
| 0,5 | 90,9 | 5,32 | 3,37 | 31,2 | 0,935 | |
| 0,718 | 63,3 | 4,44 | 2,81 | 0,82 | ||
| 0,77 | 4,3 | 2,71 | 61,2 | 0,816 | ||
| 0,79 | 5,57 | 4,16 | 2,63 | 0,805 |
Вычислим напряжения в четвертом приближении:
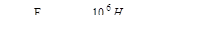 .
.
Перенапряжение составляет
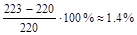
Окончательно принимаем a = 4.2 см.
Исходные данные для задачи 3.3 приняты в соответствии с рис. V.30 и таблицей V.8, а для задачи 3.4 рис. V.31 и таблица V.9.
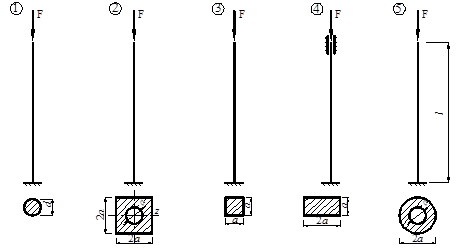

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|