
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица V.4
Таблица V.4
| схема | а | ||||||||||
| столбец | |||||||||||
q 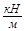
| б | ||||||||||
| F кН | в | ||||||||||
| Ме кНм | б | ||||||||||
| l м | а | ||||||||||
| h м | в | ||||||||||
| Швеллер № | 16а | б |


 Рис. V.21
Рис. V.21
Образуем основную систему (рис. V.23, а). Основная система статически определима и геометрически неизменяема. Приложив к ней внешнюю нагрузку и неизвестные усилия в «лишних» связях Х1, Х2 получим эквивалентную сис- тему (рис.15,б)

Рис. V.22

 Запишем канонические уравнения метода сил для дважды статически неопределимой системы:
Запишем канонические уравнения метода сил для дважды статически неопределимой системы:
Построим эпюру изгибающих моментов от внешних сил
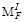 =
= 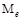 =15 кНм;
=15 кНм; 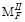 =
= 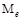 =15 кНм;
=15 кНм;
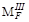 =
= 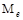 -
- 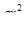
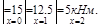
Эпюра 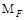 дана на (рис.V.23, г)
дана на (рис.V.23, г)
Построим эпюры изгибающих моментов ( 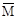 1 и
1 и 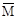 2) от единичных сил по направлению усилий
2) от единичных сил по направлению усилий 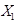 ,
, 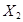 (рис. V.23, д, е).
(рис. V.23, д, е).


Рис. V.23
Определим коэффициенты канонических уравнений по правилу Вереща-гина:
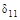 =
= 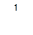
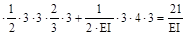 ;
; 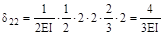 ;
;
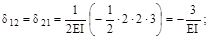
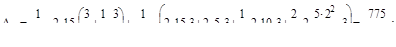
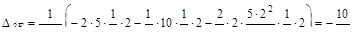 ;
;
Для проверки единичных коэффициентов построим суммарную единич-ную эпюру MS (рис. ж) путем сложения ординат эпюр 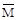 1 и
1 и 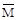 2 и «перемно-жим» ее саму на себя:
2 и «перемно-жим» ее саму на себя:

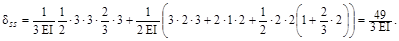
Полученный результат должен быть равен сумме «единичных» коэффи-циентов
Для проверки «грузовых» коэффициентов перемножим грузовую MF и суммарную единичную MS эпюры:
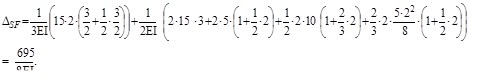
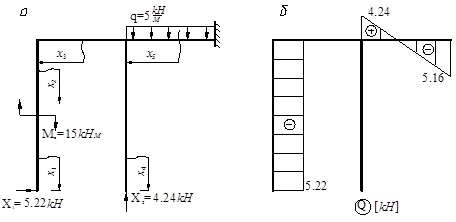

Рис. V.24
Сумма грузовых коэффициентов равна той же величине:
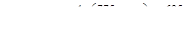 .
.
Совпадение результатов говорит о правильности расчетов.
Подставим значения коэффициентов в канонические уравнения и сокра-тим на общий множитель


Решив систему уравнений, получим : 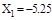 кН;
кН; 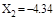 кН.
кН.
Знаки «минус», свидетельствуют о том, что принятые направления Х1 и Х2 следует изменить на противоположные.
Строим эпюры внутренних усилий N, Q, M (рис.V.24, б, в, г) с учетом найденных значений Х1 и Х2, используя метод сечений .Так, для наиболее сложного пятого участка имеем:
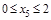 м.
м.
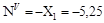 кН;
кН;
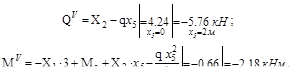
Определим экстремум
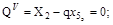
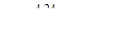
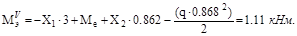 .
.
Деформационная проверка правильности найденных значений неизвест-ных Х1 и Х2 состоит в том, что мы определяем перемещение в направлении какой либо связи (Х2), «перемножив» эпюру Mz (рис. V.24, г) и 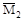 (рис. V.23, е), заранее зная, что это перемещение должны быть равным нулю.
(рис. V.23, е), заранее зная, что это перемещение должны быть равным нулю.
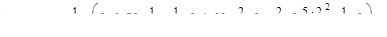
= 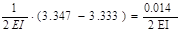
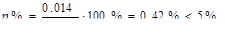
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|