
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчет статически неопределимых плоских систем.
V.2. Контрольное задание №1
1. Построить эпюры внутренних силовых факторов для заданных балок (рис. V.2, V.3), рам(рис.V.4, V.5) и вала (V.6), приняв q, F, Me, и l в соответ-ствии с индивидуальным заданием.
2. Для схемы (рис. V.2): - подобрать балку двутаврового поперечного сечения из стали, считая, что σу=240 МПа, n=1,6; 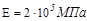 ;
;
-построить эпюры σ и τ для опасного сечения балки;
-методом начальных параметров определить прогиб в точке К (равноуда-ленной от правой и левой опоры) и построить примерный вид упругой линии.
3. Для схемы (рис. V.3) подобрать прямоугольное сечение балки из чу-гуна (если высота сечения h в два раза больше ширины b), приняв, 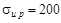 МПа,
МПа, 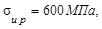 n =2. Построить эпюры σ и τ для опасного сечения балки.
n =2. Построить эпюры σ и τ для опасного сечения балки.
4. Для схемы (рис. V.4) проверить прочность составного сечения, представленного на схеме (рис. V.6) , полагая σadm=160 МПа.
5. Для схемы (рис. V.7) подобрать размеры сплошного круглого вала на каждом из участков, полагая, что на левом участке вал кольцевого сечения и дать эскиз вала.
Таблица V.1
| Схема | а | ||||||||||
| столбец | |||||||||||
| F kH | 14 | б | |||||||||
q 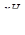
| 6 | в | |||||||||
| Me kHм | 12 | а | |||||||||
| l м | 2.2 | 2.4 | 2.6 | 2.0 | 2.8 | 3.0 | 2.0 | 2.4 | 2.6 | 3.0 | б |
| h м | -2.5 | в |
В таблице V.1 даны исходные данные для расчётных схем изображённых на рис. V(2,3,4,5). К примеру, если последние три цифры вашей зачётки 137, то следует решать задачу по схеме №7, приняв F = 14кH, q = 6 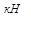 Me=12
Me=12 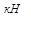
l =2.6м, h = 2м.





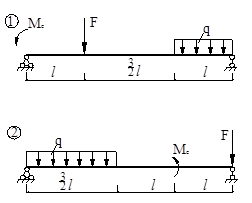
Рис. V.2


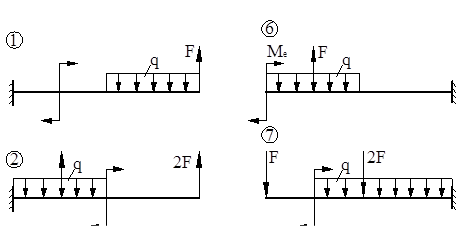
Рис. V.3


 Рис. V.4
Рис. V.4





|



|
|
| строка | Полоса | Швеллер | Двутавр | Равнобокий уголок |
| Схема рис.V.6 | ||||
300 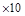
| 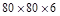
| |||
310 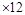
| 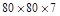
| |||
280 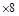
| 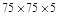
| |||
280 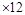
| 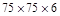
| |||
320 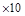
| 18а | 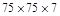
| ||
320 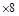
| 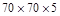
| |||
320 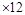
| 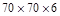
| |||
300 
| 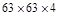
| |||
300 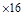
| 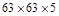
| |||
300 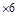
| 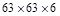
| |||
| а | б | в | а | б |


 Рис. V.7
Рис. V.7
Таблица V.3
| схема | а | ||||||||||
| столбец | |||||||||||
| Ме кНм | б | ||||||||||
| τadm МПа | в | ||||||||||
| d/D | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.9 | 0.8 | 0.6 | 0.5 | б |
Рассмотрим некоторые типовые примеры. Для балки (рис. V.8) исходные данные:
F =12 кН; q = 6 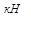
Me=18 кНм; l =6 м.

  Рис. V.8 Рис. V.8
|
Изобразим расчетную схему балки, указав длины участков, величины внешних нагрузок и направления реакций. Левая опора А – шарнирно - подвиж-ная, и в ней в общем случае могут быть вертикальная составляющая реакции RA и горизонтальная -HA. Правая опора - шарнирно-подвижная и в ней вертикальная реакция RB.
Чтобы составить выражения для Q, M, предварительно следует опреде-лить реакции опор.
Спроектировав все силы на горизонтальную ось x, установим, что HA=0.
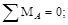
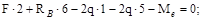 RB=11 kH.
RB=11 kH.
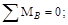
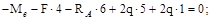 RA=1 kH.
RA=1 kH.
Проверка: 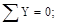
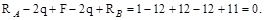
Полученные знаки «плюс», свидетельствуют о правильном выборе нап-равлений для RA и RB. Если реакция получена со знаком «минус», следует из-менить направление ее вектора на противоположное.
Имеем три участка. Проведем в них сечения и покажем текущие коорди-наты. Для первого участка рассмотрим в равновесии левую часть, а для второго и третьего- правую.
Участок I ( 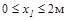 )
)
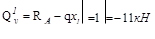 ;
;
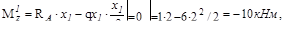
где qx1 - равнодействующая распределенной нагрузки, а 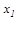 - плечо этой силы.
- плечо этой силы.
Величина 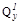 линейно зависит от x, поэтому достаточно двух значений для построения эпюры Qy. Закон изменения
линейно зависит от x, поэтому достаточно двух значений для построения эпюры Qy. Закон изменения 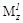 - параболический, и для пос-троения эпюры
- параболический, и для пос-троения эпюры 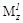 необходимо иметь по крайней мере три значения.
необходимо иметь по крайней мере три значения.
Дифференциальная зависимость при изгибе  позволит заклю-чить, что экстремальное значение функции
позволит заклю-чить, что экстремальное значение функции 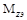 будет при
будет при 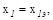 которое следует определить из условия Q=0:
которое следует определить из условия Q=0:
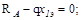
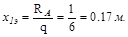
Таким образом,
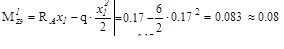 кHм
кHм
Положительные значения Qy откладывают над базовой линией. Положи-тельные значения изгибающих моментов Mz откладывают под базой (строят Mz на «растянутом волокне»). Вспомним, что изгибающий момент принято счи-тать положительным в случае, если растянуты нижние слои балки.
Участок II ( 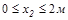 )
)
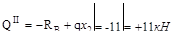
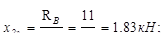
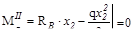
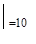
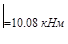
Участок III ( 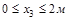 )
)
Распределенная нагрузка на соседнем (втором) участке представляется в виде равнодействующей 2q, приложенной в середине этого участка. Таким образом,
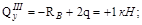
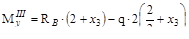
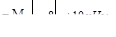
Эпюры Qy и Mz представлены на рис. V.8, б, в.
Обратим внимание, что в сечениях, где приложены сосредоточенные си-лы RA, F, RB на эпюре Qy имеем скачки на величину этих сил в направлении сил (если двигаться слева направо).
На третьем участке распределенная нагрузка отсутствует и величина 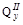 постоянна,
постоянна, 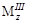 изменяется по линейному закону. Площадь эпюры равна
изменяется по линейному закону. Площадь эпюры равна 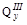 =1кН·2м =2кHм, и изменение изгибающего момента
=1кН·2м =2кHм, и изменение изгибающего момента 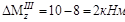 . На этом участке
. На этом участке 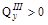 и
и 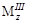 изменяется от - 10 кНм до 8 кНм, т.е. увели-чился на 2 кНм.
изменяется от - 10 кНм до 8 кНм, т.е. увели-чился на 2 кНм.
На первом участке длинной 2м имеем 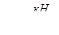 и по мере возрастания x поперечная сила уменьшается от +1 до -11кН (на 12 кН) по линейному закону. Изгибающий момент изменяется по закону параболы с экстремальным значением 0,08 в сечении, где
и по мере возрастания x поперечная сила уменьшается от +1 до -11кН (на 12 кН) по линейному закону. Изгибающий момент изменяется по закону параболы с экстремальным значением 0,08 в сечении, где 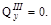
В сечении С приложена пара сил Me=18 кНм, которая растягивает верх-ние волокна, и на эпюре Мz, при переходе со второго на третий участок, име-ем скачок на -18кНм.
Для консоли, изображенной на рис. V.9,а, эпюры Qy и Mz можно пос-троить без определения реакций, если для каждого участка рассматривать часть балки, не содержащую опору.
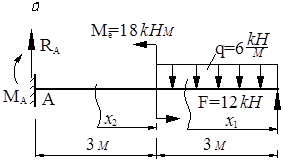


|
Участок I ( 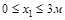 )
)
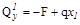

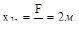

Участок II ( 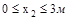 )
)
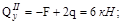
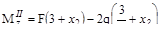
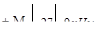
Построив эпюры (рис. V.9, б, в), следует провести анализ аналогичный тому который имел место в предшествующей задаче.
Перейдем к построению эпюр внутренних усилий в ломанных брусьях (рис.V.4,5). В общем случае в поперечных сечениях возникают три внутренних силовых фактора: продольная сила N, поперечная сила Qy и изгибающий мо-мент Mz. Вводится подвижная прямоугольная система координат и каждый участок рассматривается как балка. Правильность построения эпюр Mz контро-лируют условием равновесия узлов.
Построению эпюр для шарнирно опертого бруса (рис.V.10, а) должно предшествовать определение реакций:
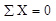 ;
;  ;
; 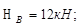
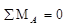 ;
; 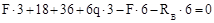 ;
; 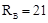 кН;
кН;
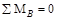 ;
; 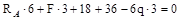 ;
; 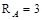 кН;
кН;
Проверка: 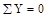 :
: 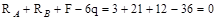 .
.





Рис. V.10
Имеем три участка. Направления обхода обозначены на рисунке.
Участок I ( 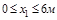 )
)
N=0; 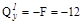 кН;
кН;
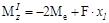
При 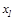 =0 изгибающий момент растягивает верхние волокна, и ординату Mz = - 36 кНм откладываем сверху; при x1= 6 растягиваются нижние волокна (ордината Mz= +36 кНм - снизу). На эпюре Mz знак не ставят, так как расположение эпюры на «растянутом волокне» дает исчерпывающую информацию.
=0 изгибающий момент растягивает верхние волокна, и ординату Mz = - 36 кНм откладываем сверху; при x1= 6 растягиваются нижние волокна (ордината Mz= +36 кНм - снизу). На эпюре Mz знак не ставят, так как расположение эпюры на «растянутом волокне» дает исчерпывающую информацию.
Участок II ( 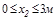 )
)
Используем правило знаков для правой части бруса
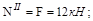
 кН;
кН;
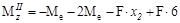
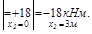
В начальном сечении второго участка Mz растягиваются правые волокна (эпюра-справа), в конечном сечении- левые волокна (эпюра- слева). Эпюра Qy строится в соответствии с принятой ранее ориентацией вертикального участка в отношении правила знаков.
Участок III ( 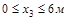 )
)
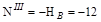 кН;
кН; 
Определим значение х3э, при котором 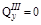 :
:
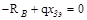 ;
; 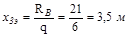 ;
;
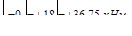
Эпюры представлены на рис.V.10 б, в, г. Эпюра Mz на участке III - парабола, выпуклость которой направлена в сторону действия распределенной нагрузки q.
Для проверки правильности построения эпюры Mz выделим узлы А и С посредством сечений, бесконечно близких к точкам А и С .
В узле А ( рис. V.10, e) не приложена внешняя пара сил и, рассматривая эпюру Mz, можно отметить, что вертикальный стержень в непосредственной близости от узла растянут слева моментом 18 кНм, а горизонтальный стержень растянут снизу моментом 18 кНм. Точкой обозначено растянутое волокно стер-жня, стрелкой - направление момента, который вызвал это растяжение. Следо-вательно, узел А находится в равновесии.
В узле С ( рис.V.10,д) приложена внешняя пара сил Mz=18 kHм, направ-ленная по часовой стрелке. Вертикальный стержень изгибается моментом 18 кНм (эпюра справа), который растягивает правое волокно, а горизонтальный стержень - моментом 36 кНм, растягивающим нижнее волокно. Суммируя упомянутые моменты можно заключить, что условие равновесия узла С соблюдается.
Для рамы, имеющей защемленную опору (рис. V.11, а) эпюры N, Qy, Mz можно построить, не определяя реакции опоры (MA, HA, RA). Обход участков следует вести со стороны свободного конца.
Участок I ( 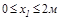 )
)
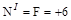 кН;
кН;
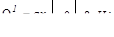
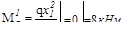
Участок II ( 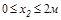 )
)
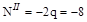 кН;
кН; 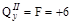 кН;
кН;
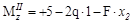
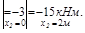
Участок III ( 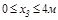 )
)
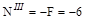 кН;
кН; 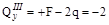 кН;
кН;
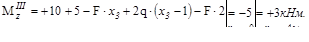




|
Узел В
Эпюры N, Qy, Mz, показаны на рис. V.11, в, г, д.
Моменты относительно оси z3 создают пять внешних нагрузок. Пос-кольку в равновесии рассматривается правая часть рамы, то правило знаков для Mz (Mz > 0) позволяет заключить, что обе пары сил и распределенная нагрузка дают положительные составляющие в выражении для моментов, а силы F, при-ложенные в точках В и Д - отрицательные. Распределенную нагрузку участка СД следует заменить равнодействующей 2q, тогда плечо этой силы (x3-1).
Условие равенства нулю в узлах B и C показаны на рис. V.11, е, ж.
Переходя к расчетам на прочность следует вспомнить, что допускаемое напряжение
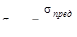
получают уменьшая предельное напряжение в n раз, где n - коэффициент запа-са.
Для пластичных материалов предельное напряжение - предел текучести – σу, а для хрупких временное сопротивление –σu. Для хрупких материалов, имеющих существенно отличающиеся ( в несколько раз) временное сопротив-ление сжатию 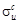 и временное сопротивление растяжению
и временное сопротивление растяжению 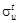 проводят про-верку безопасной прочности в сжатой и растянутой областях.
проводят про-верку безопасной прочности в сжатой и растянутой областях.
В соответствии с пунктом 2 контрольного задания №1 подберем балку двутаврового поперечного сечения из стали с 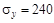 МПа; при n = 1,6. Усло-вие безопасной порочности имеет вид:
МПа; при n = 1,6. Усло-вие безопасной порочности имеет вид:
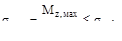 .
.
Величину Mz,мах=10.08 кНм берем из эпюры (рис.V.8, в), а допускаемые напряжения равны.
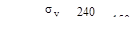 МПа.
МПа.
Определим осевой момент сопротивления:
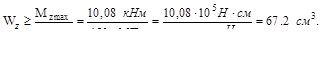
По сортаменту ГОСТ 8239-89 выбираем двутавр № 14 (рис.V.12, а), у которого осевой момент сопротивления ближайший больший к расчетному значению. Выпишем параметры I № 14: h =14 см; b = 7.3см; S = 0.49 см; t = 0.75 см; A=17.4 см2; Iz=572 см4; Wz=81 см3 ; 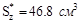 .
.
Определим величину σмах, если балка будет изготовлена из I №14, в сече-нии с наибольшим изгибающим моментом.
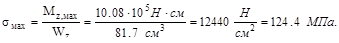
Наибольшие касательные напряжения будут в сечении, где самая боль-шая по абсолютной величине поперечная сила Q = 11 кН (из эпюры рис.V.8, б).
Касательные напряжения в любой точке сечения при поперечном изгибе определяют по формуле Журавского:
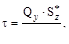 где Q- поперечная сила, Iz - момент инерции сечения,
где Q- поперечная сила, Iz - момент инерции сечения, 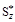 - статический момент отсеченной части, b(y) - ширина сечения, измеренная по линии, параллельной оси z, проходящей через искомую точку.
- статический момент отсеченной части, b(y) - ширина сечения, измеренная по линии, параллельной оси z, проходящей через искомую точку.
Наибольшего значения напряжений 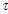 достигает на нейтральной оси се-чения:
достигает на нейтральной оси се-чения:
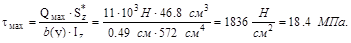 .
.
Для вычисления τ в точке L сечения стенки в месте перехода ее в полку следует определить статический момент осеченной части (полки).
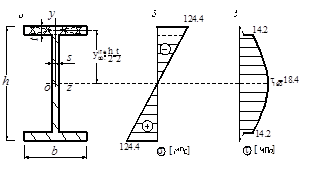
Рис. V.12
Зная характер изменения σ (линейный) и τ (параболической) по высоте сечения, строим эпюры (рис.V.12, б, в).
Расчет на прочность балки при изгибе должен обеспечить ее безопасную прочность, но это не гарантирует необходимую жесткость балки. Определяют максимальные прогибы балки, которые не должны превышать значений проги-бов, устанавливаемых в соответствии с её эксплуатационным назначением.
Существует несколько способов определения перемещений. Используем метод начальных параметров с универсальной формулой:
EIV=EIVo+EI 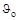 x+
x+ 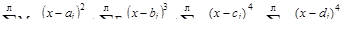
где:  Mi, Fi, qi - внешние нагрузки, включающие и опорные реакции, распо-ложенные левее (знак «Л» над знаком суммы) от рассматриваемого сечения;
Mi, Fi, qi - внешние нагрузки, включающие и опорные реакции, распо-ложенные левее (знак «Л» над знаком суммы) от рассматриваемого сечения;
ai, bi, сi, di- расстояния от начала координат до сечения, где приложены эти нагрузки;
V - перемещение центра тяжести сечения по направлению, перпендикулярному оси балки x (если перемещение вверх по оси y, то V > 0);
Vo - перемещение в начале координат О;
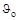 - угол поворота сечения в начале координат по отношению к исходному (ненагруженному)положению. Если поворот против часовой стрелки, по
- угол поворота сечения в начале координат по отношению к исходному (ненагруженному)положению. Если поворот против часовой стрелки, по 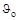 >0.
>0.

Рис. V.13
Начальные параметры Vo и 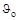 определяют из граничных условий (огра-ничений, накладываемых опорами).
определяют из граничных условий (огра-ничений, накладываемых опорами).
В соответствии с условиями вывода формулы начало координат О при-нято располагать в крайнем левом сечении балки (сохраняя его общим для всех участков), ось y направлять вверх, а ось x - вправо (рис. V.13). Внешние силы, показанные на этом рисунке, принимаются положительными, (они вызывают изгибающие моменты, растягивающие нижнее волокно). Если направления внешней силы противоположно, то в уравнении прогибов ее записывают со знаком «минус».
Определим перемещение точки К балки. Расчетная схема и эпюра Мz приведена на рис.V.14, а, б.
  
| Граничные условия в данном слу-чае имеют следующий вид:
а) VA=0, при Х=0;
б) VB=0, при Х=6м,
(опоры не позволяют балке перемещать-ся в точках А и В в вертикальном направ-лении.
Левая опора совпадает с началом координат VА=Vо=0. Следовательно один из начальных параметров определен.
Для нахождения второго ( 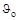 ), ис-пользуем условие (б).
В уравнение должны войти все внешние усилия, расположенные левее сечения В. ), ис-пользуем условие (б).
В уравнение должны войти все внешние усилия, расположенные левее сечения В.
|
Рис. V.14 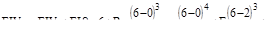
 .
.
В сечении С распределенная нагрузка обрывается, поэтому для восста-новления силовой схемы начиная с сечения С и до правого конца балки вводят «компенсирующую нагрузку» q противоположного направления (что показано пунктиром), которая учитывается слагаемым + 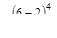 . Нагрузка q на учас-ток NB находит отражение в слагаемом
. Нагрузка q на учас-ток NB находит отражение в слагаемом 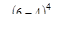 . Таким образом получаем:
. Таким образом получаем:
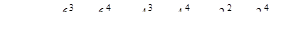 ;
;
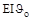 =10.67 кНм2.
=10.67 кНм2.
Итак, 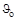 >0, следовательно, сечение в начале координат поворачивается против часовой стрелки (рис.V.14, в).
>0, следовательно, сечение в начале координат поворачивается против часовой стрелки (рис.V.14, в).
Для определения прогиба в точке К (при х=3м) составим уравнение:
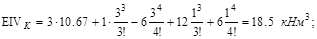
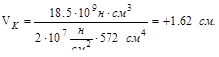 .
.
Таким образом точка К перемещается вверх на 1.62 см.
Дополнительную информацию можно получить, исследуя характер эпю-ры Мz. Так на участках AL и NB эпюра расположена под базовой линией, следо-вательно растянуты нижние волокна и кривизна упругой линии (эпюры проги-бов) положительна (кривая обращена вогнутостью вверх). На участке LN - вверх, так как эпюра моментов расположена над базовой линией, растянуты верхние волокна, и кривизна упругой линии отрицательна (кривая обращена вогнутостью вниз).
Выполняя п.3 контрольной работы №1 ,следует из эпюры для схемы V.3 взять наибольшее значение Мz,max. Пусть, например, Мz,max=49 кНм, Qy,мах= 15 кН.
Допускаемы значения напряжений в растянутой и сжатой зонах:

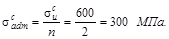 .
.
Момент сопротивления для прямоугольника 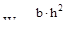 при заданном соотношении размеров сторон h = 2b равен:
при заданном соотношении размеров сторон h = 2b равен:
 .
.
Из условия безопасной прочности в растянутой зоне
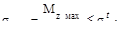
следует, что момент сопротивления, обеспечивающий безопасную прочность,
будет
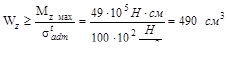 ,
,
и необходимые размеры прямоугольника определяем так:
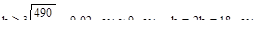
Для сжатой зоны условие безопасной прочности имеет вид:
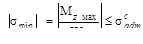 ,
,
откуда следует:
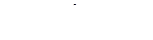 ,
, 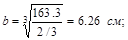 h=12,5 см.
h=12,5 см.
Поскольку сечение с такими размерами не обеспечит прочность в растянутой зоне, окончательно принимаем: h=18 см; b=9 см.
Построим эпюры σ и τ. Вычислим наибольшие напряжения:
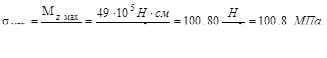
|
 Это на 0,8% превышает
Это на 0,8% превышает 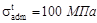 .Принято считать, что если пере-грузка не превышает 5% от допустимого напряжения, то безопасная прочность обеспечена.
.Принято считать, что если пере-грузка не превышает 5% от допустимого напряжения, то безопасная прочность обеспечена.
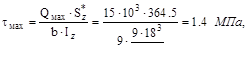
где 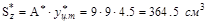 (рис.V.15, а); а Qmax - взято из эпю-ры (принято 15 кН).
(рис.V.15, а); а Qmax - взято из эпю-ры (принято 15 кН).
Эпюры σ и τ даны на рис. V.15, б, в.
В пункте 4 контрольного задания и №1 требуется проверить прочность балки составного сечения, изображенного на схеме рис. V.6. полагая 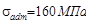 .
.
В условие безопасной прочности входит осевой момент сопротивления Wz, вычислив который сможем сделать заключение о прочности.
Изобразим в масштабе выбранное по рис. V.6 и таблице V.2 сечение, к примеру, в соответствии с рис. V.16, воспользовавшись таблицами сортамента, прокатной стали, которые приведены в приложениях I, II, III.
| Швеллер №30 ГОСТ 8240-89 | h=30 см, b=10 см, S=0.65 см, t=1.1см, А1=40.5 см2,
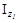 =327см, уo=2.52см. =327см, уo=2.52см.
|
| Двутавр №30 ГОСТ 8239-89 | h=30 см, b=13.5 см, S=0.65 см, t=1.02 см, А2=46.5 см2,
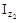 =7080 см4, =7080 см4,
|
Осевой момент сопротивления необходимо вычислить относительно гла-вной центральной оси инерции zo. Поэтому на первом этапе следует определить положение центра тяжести поперечного сечения, состоящего в данном случае из швеллера №30 (элемент 1) и двух двутавров (элементы 2 и 3 на рис. V.16).
Выберем произвольную систему координат yz таким образом, чтобы все элементы сечения располагались в первом квадранте. Обозначим центры тяжести каждого элемента (О1, О2, О3) и определим их координаты в осях y, z:
 для швеллера: у1=30+(10-2.52)=37.48 см;
для швеллера: у1=30+(10-2.52)=37.48 см; 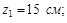
 для двутавров у2= у3 =15 см;
для двутавров у2= у3 =15 см; 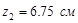 ;
; 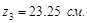
Координата центра тяжести по оси z в силу симметрии сечения равна 15 см, а координату уо определим по известной формуле:
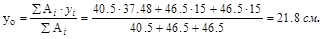

Рис. V.16
Итак, оси yo, zo являются главными центральными осями инерции. Ис-пользуя формулу: 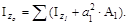
определим величину главного центрального момента инерции всего сечения. Координаты центров тяжести элементов в системе центральных осей yo, zo:
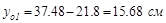
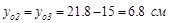
Таким образом:
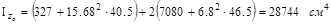
момент сопротивления равен
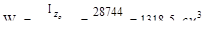
где 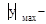 расстояние наиболее удаленной точки сечения от оси zo.
расстояние наиболее удаленной точки сечения от оси zo.
Максимальный изгибающий момент для консольной балки (рис. V.9, в) равен 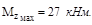
Условие безопасной прочности:
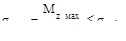
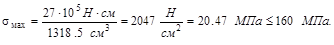
Безопасная прочность обеспечена.
В пункте 5 контрольного задания №1 требуется подобрать размеры спло-шного круглого вала на каждом из участков, полагая, что левый участок кольцевого сечения, к примеру 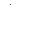 а
а 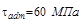 .
.
Рассмотрим пример (рис V.17, а):
Вал имеет три участка.
Проведем сечения на каждом участке и будем рассматривать равновесие
правых частей вала. Это позволит построить эпюры Т не определяя величину момента МА в опоре.
T I=18 кНм;
Т II=18+36=54 кНм;
Т III=18+36-18=36 кНм.
Эпюра дана на рис. V.17, б.
Эскиз вала дан на рис.V.17, в.



Рис. V.17
Из условия безопасной прочности при кручении:
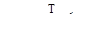 ,
,
где 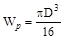 , Определяем необходимый диаметр вала для каждого участка по формуле
, Определяем необходимый диаметр вала для каждого участка по формуле 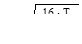 .
.
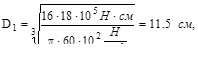 аналогично D2=16.6 см;
аналогично D2=16.6 см;
Для кольцевого сечения 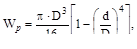 тогда
тогда
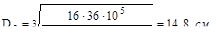 а d3 = 0.5D3 = 7.4 см.
а d3 = 0.5D3 = 7.4 см.
Контрольное задание №2
Расчет статически неопределимых плоских систем.
Задача 2.1. Для неразре
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|