Предварительные элементарные преобразования подынтегральной функции

Предварительные элементарные преобразования подынтегральной функции

До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)

Конечно, мы делали кое-какие простенькие преобразования – множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)

А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. :)

Применение формул тригонометрии

Продолжим развлекаться с тригонометрией.

Пример 9

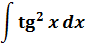
Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:

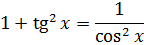
Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:

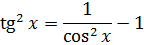
Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!

Смотрите:

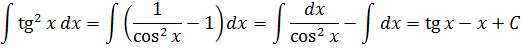
А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать – применять формулу производной сложной функции:

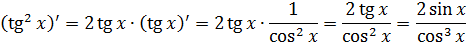
И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.

А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование – более творческий процесс, нежели дифференцирование.

12 3 4 Следующая ⇒