Вычисление свободных членов уравнений поправок

4. Вычисление свободных членов уравнений поправок

Свободные члены вычисляются по формуле (1.12), которая в Excel имеет вид, приведенный на рис.1.14

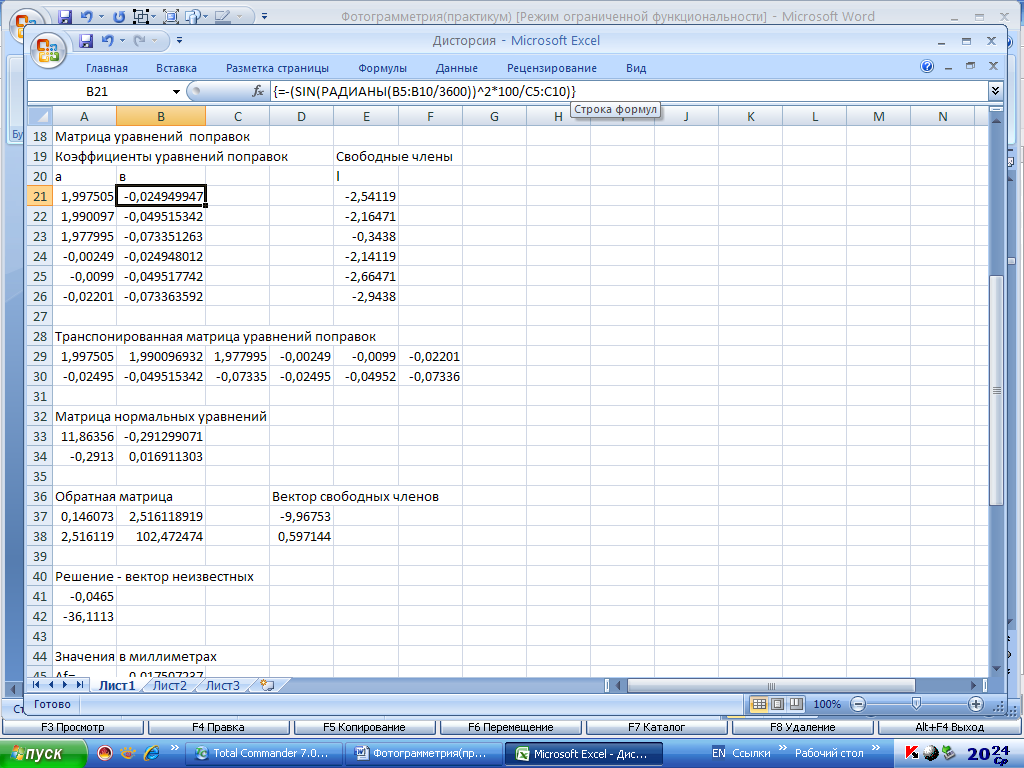
Рис.1.13. Вычисление коэффициентов в

Рис.1.14. Вычисление свободных членов

5. Составление нормальных уравнений и их решение

Нормальные уравнения составляются в соответствии с (1.23),(1.24), и в соответствии с (1.25) решаются. При этом в Excel выполняются следующие действия (рис.1.15):

- составляется транспонированная матрица,

-составляется матрица нормальных уравнений,

- находится обратная к ней матрица,

-составляется решение в соответствии с (1.25).

Транспонированная матрица составляется библиотечной функцией ТРАНСП()(рис.1.15). Матрица нормальных уравнений строится библиотечной функцией МУМНОЖ() умножения транспонированной матрицы А´ на исходную А (рис.1.16). Обращение матрицы нормальных уравнений осуществляется функцией МОБР()(рис. 1.17). Каждая из этих функций завершаются следующей командой ОК→ F2→Ctrl+Shift +ENTER

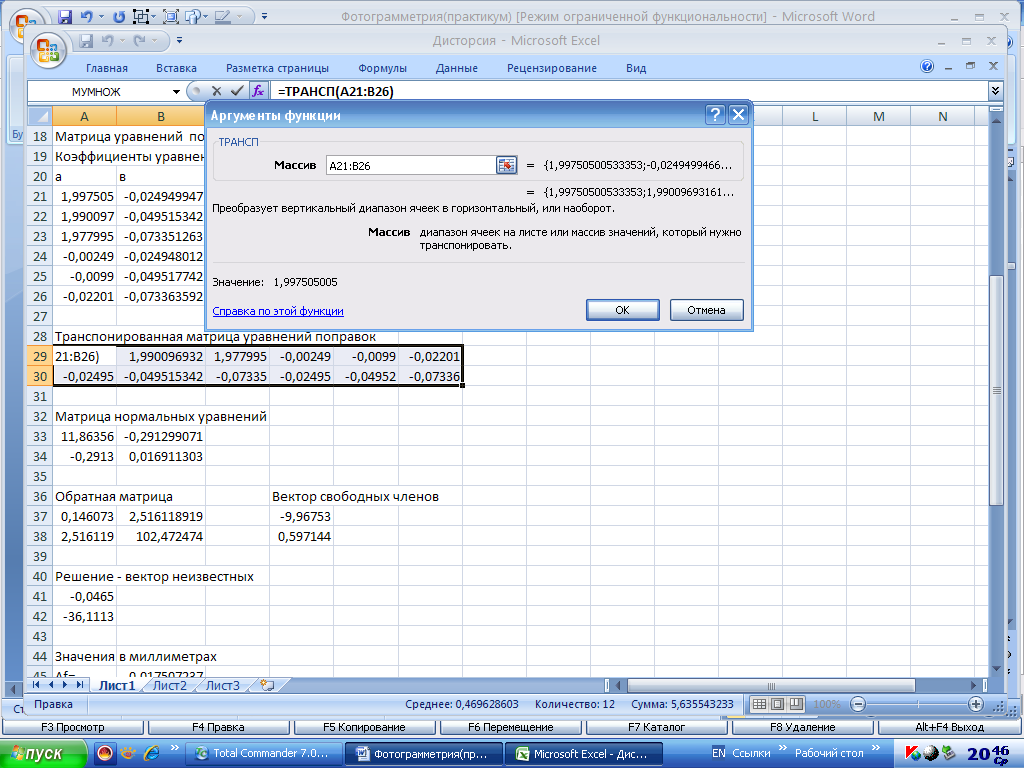
Рис. 1.15. Функция транспонирования матрицы

Рис. 1.16. Построение матрицы нормальных уравнений

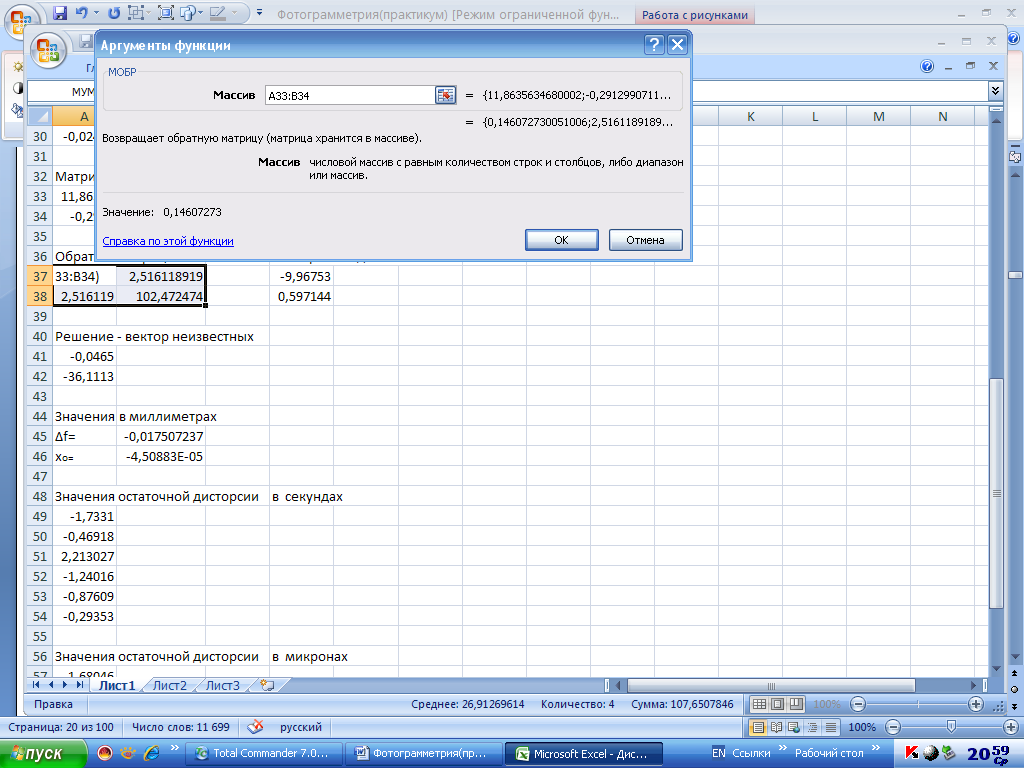
Рис. 1.17. Обращение матрицы нормальных уравнений

Для получения решения находится вектор A´L, формула вычисления которого приведена на рис.1.18. Само решение осуществляется в соответствии с (1.25) по формуле, приведенной на рис. 1.19

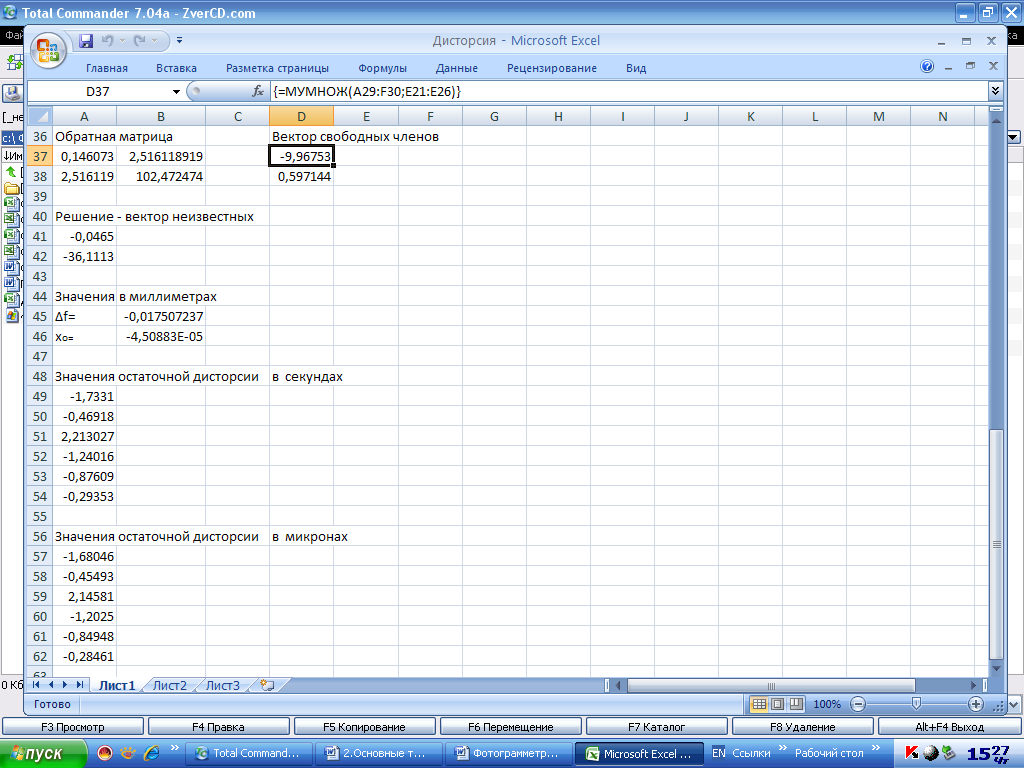
Рис.1.18. Вычисление вектора A´L

Рис.1.19. Решение

Для представления решения в миллиметрах осуществляется перевычисление

на основании формул (1.16):

Δf=v۰100/206265,

xo=u۰fo/206265.

В Excel перевычисление осуществляется по формулам, приведенным на рис.1.20, 1.21.

Рис.1.20. Вычисление Δf

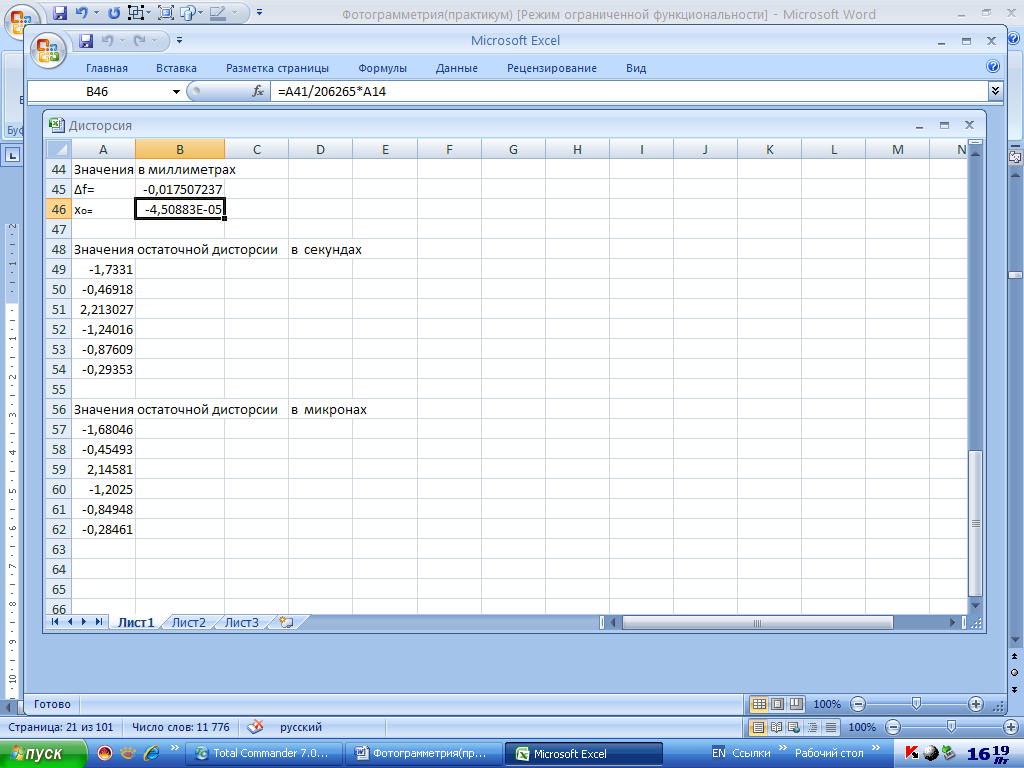
Рис. 1.21. Вычисление xo

Окончательный результат следующий:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒