
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение элементов внутреннего ориентирования снимка и дисторсии изображения
1.4.Определение элементов внутреннего ориентирования снимка и дисторсии изображения
Задача определения дисторсии изображения и элементов внутреннего ориентированиясъемочной камеры называется фотограмметрической калибровкой аэрофотоаппарата (АФА). Существуют следующие способы калибровки
Существуют следующие методы калибровки:
1. визуальный
2. фотографический
3. полевой
1.4.1.Визуальный способ калибровки АФА.
В визуальном способе измеряются углы, нанесенные на выравнивающем стекле оптико-механического устройства.
Схема измерений приведена на рисунке 1.9. Здесь а - метка,
b – видимое изображение метки, f – фокусное расстояние аэрофотоаппарата. Дисторсия равна разности
δ=oa-bo;
Поскольку
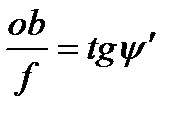 ,
, 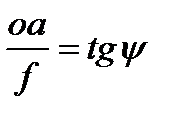 ,
,
то очевидно, что
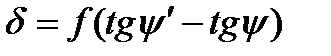 ;
;
Обозначая
f tgψ =r
запишем
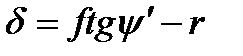 . (1.7)
. (1.7)
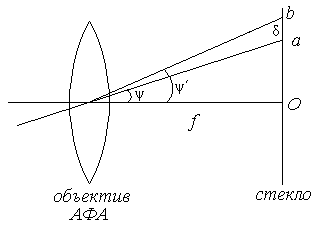
Рис.1.9. Дисторсия аэрофотоаппарата
Поскольку в данном уравнении два неизвестных- δ, f – то фокусное расстояние находят при условии 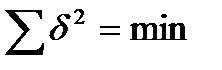 , т.е записывается следующая минимизирующая функция.
, т.е записывается следующая минимизирующая функция.
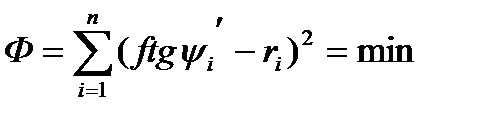 .
.
В таком случае производная этой функции по фокусному расстоянию равна нулю
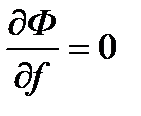 .
.
Тогда будет справедливо равенство
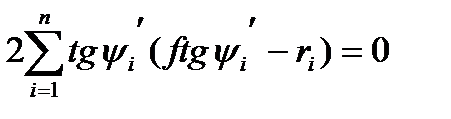 ,
,
или
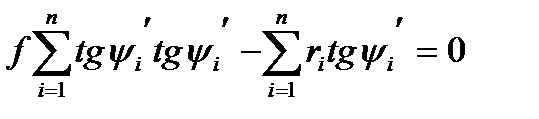 , (1.8)
, (1.8)
из которого находится фокусное расстояние.
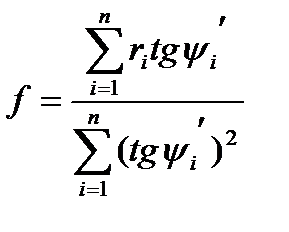 . (1.9)
. (1.9)
Описанный способ является оценочным и не полным, так как в нем не определяются координаты главной точки снимка. Для совместного определения элементов внутреннего ориентирования и дисторсии измеряют углы W(рис.1.10) в вершине задней узловой точки объектива между марками контрольной сетки. Сама сетка помещается в фокальной плоскости АФА.
| r |
| xo |
| S |
| О |
| В1 |
| В2 |
| В3 |
| C |
| А1 |
| А2 |
| θ |
| W |
| ψ |
| f |
Рис. 1.10. Визуальный способ определения элементов внутреннего ориентирования АФА.
Измеренные углы W связаны с определяемыми элементами следующим образом:
W=-θ(xo)+ψ(r,f)
для точек слева от центра С сетки и
W=θ(xo)+ψ(r,f)
для точек справа от этого центра.
Очевидно, что можно записать следующее уравнение, связывающее измеренный угол с неизвестными f, xo.
W= θ(xo) +arctg(r/f). (1.10)
Для записи его в линейном виде введем обозначения
f=fo+Δf,
r=ro+Δr,
где fo, ro – приближенные значения фокусного расстояния f и отрезка r, Δf, Δr – поправки к ним. Через u обозначим поправку в измеренный угол W. В качестве приближенного значения угла θ примем нуль.
Тогда уравнение (1.10) в разложении в ряд Тейлора можно записать так
W+u= arctg(ro/fo)+θ+(fo²/(ro²+fo²))(Δr/fo)-(r/(ro²+fo²))Δf.
Для удобства вычислений его несколько преобразуют
W+u= arctg(ro/fo)+θ(xo)+(fo²/(ro²+fo²))(Δr/fo)-(ro²/(ro²+fo²))(Δf/ro
Поскольку
fo²/(ro²+fo²))=cos²W,
ro²/(ro²+fo²)=sin²W,
то это уравнение будет иметь такой вид
W+u= arctg(ro/fo)+ θ(xo )+ cos²W (Δr/fo)- sin²W (Δf/ro),
или
u= θ(xo )+ cos²W (Δr/fo)- (sin²W۰100/ ro)۰(Δf/100)+l, (1.11)
где
l= arctg(ro/fo)-W. (1.12)
Положим, что
Δr=xo,
θ(xo )= xo/f= Δr/f, (1.13)
Дифференциалом угла θ примем сам этот угол, дифференциалом xo= Δr
примем Δr .
Тогда дифференциал выражения (1.13) будет
Θ= Δr/f- ΔrΔf /f², (1.14)
Полагая приближенное значение Δr равным нулю, (1.14) перепишем так
Θ= Δr/f.
После подстановки его в (1.11) получим окончательный вид уравнения связи измеренной величины W и неизвестных Δr/fo, Δf/100:
-для точек справа от центра С
u= (1+ cos²W) (Δr/fo)- (sin²W۰100/ ro)۰(Δf/100)+l, (1.15)
и
u= (-1+ cos²W) (Δr/fo)- (sin²W۰100/ ro)۰(Δf/100)+l (1.16)
-для точек слева от центра С.
В общем виде эти уравнения можно записать так
u= a ۰(Δr/fo)- b ۰ (Δf/100)+l . (1.17)
Для удобства изложения введем следующие обозначения
u= Δr/fo, v= Δf/100. (1.18)
а (1.17) перепишем в матричном виде
АХ+L=V , (1.19)
где
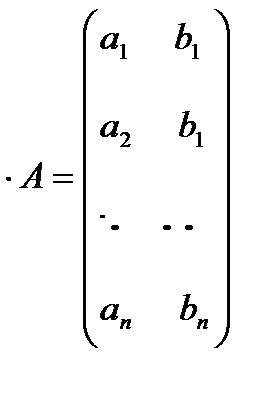 ,
, 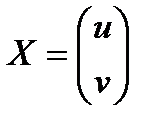 ,
, 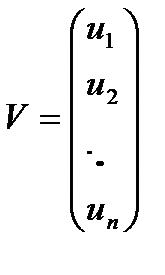 (1.20)
(1.20)
Уравнений вида (1.17) составляется столько, сколько измеряется углов W.
Решаются они по методу наименьших квадратов, т.е. при следующем экстремуме:
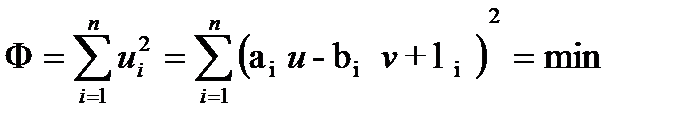 (1.21)
(1.21)
В точке экстремума производные функции (1.21) по переменным должны равняться нулю:
dФ/du= 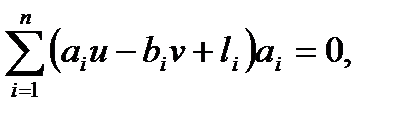
dФ/dv= 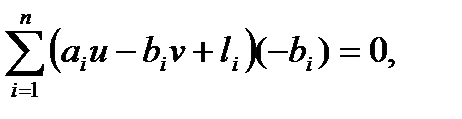 (1.22)
(1.22)
Выражениям (1.22) соответствует следующая система нормальных уравнений



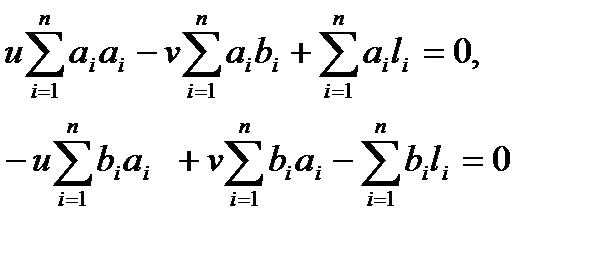 , (1.23)
, (1.23)
матричный вид которой следующий
NX+AL=0 , (1.24)
где N =A´A, а А´ -транспонированная матрица.
Из решения (1.21) находятся u и v. В матричном виде это такое решение
X=-Nֿ¹A´L, (1.25)
где Nֿ¹ - обратная к N матрица
а по ним из (1.18) Δr и Δf.
Значение Δr равнохо, а фокусное расстояние вычисляется по формуле
f=fo+ Δf.
После подстановки вектора неизвестных в (1.19) находят вектор V остаточной дисторсии.
Отметим, что в частном случае при Δr=0 система (1.23) преобразуется в (1.8).
Это легко проследить по выражениям (1.15),(1.16), приняв в них
ro=fo tgWo
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|