
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
АНАЛІЗ ПЕРЕХІДНИХ ПРОЦЕСІВ ПРИ РЕГУЛЮВАННІ 3 страница
Перехідні процеси в парогенераторах не враховуються, тому що вони протікають набагато повільніше, ніж в АСРЧ і П.
Передбачається, що апаратура АРЧ і П ідеально реалізує заданий закон регулювання, тому динамічні параметри конкретної апаратури не враховуються.
При цих допущеннях структурна схема АРЧ і П для малих відхилень змінних величин наведена на рис. 3.4 [10].
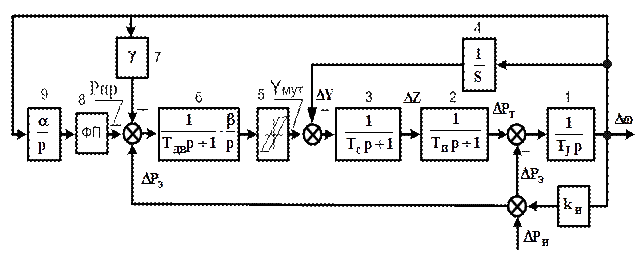
Рисунок 3.4 - Структурна схема AСР частоти і потужності за пропорційно-інтегральним відхиленням в енергосистемі з теплових електростанцій
Інтегруюча ланка 1 представляє обертові маси енергосистеми зі сталою часу ТJ. Зворотний зв'язок, що охоплює цю ланку, ураховує регулюючий ефект навантаження. Передатна функція нерегульованої енергосистеми записується у вигляді:
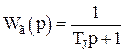 .
.
Для реальних енергосистем ТJ ≈ 10 с. Коефіцієнт регулюючого ефекту навантаження (kн =ΔР*/Δf*) залежить від состава споживачів енергосистеми. Для різних енергосистем з характерним для них составом споживачів kн різний і перебуває в межах 1 ¸ 3 [10]. Це значить, що при зниженні частоти на 1% (0,5 Гц) споживання активної потужності зменшиться на 1 ¸ 3 %, а при підвищенні частоти збільшиться на 1 ¸ 3 %.
Інерційна ланка 2 відображає процес перетворення потужності потоку енергоносія в потужність на валу турбоагрегату. При незмінному тиску пару перед турбіною витрата пару, що визначає потужність на валу, залежить тільки від зміни відкриття регулювального клапана або положення поршня сервомотора (див. рис.3.1). Інерційність ланки визначається паровим об'ємом, що розташований між регулювальним клапаном і першим рядом сопел турбіни, характеризується сталою часу Tп. Чисельно величина Tп становить 0,2 ¸ 0,4 с. Передатна функція турбіни має вигляд:
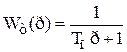 .
.
Ланки 3 і 4 представляють АРЧО. Вимірювальна частина регулятора приймається ідеальною і описується передатним коефіцієнтом 1/S, що зв'язує відхилення частоти Δω на вході ланки 4 з сигналом DY (наприклад, зсув муфти відцентрового регулятора). На виході ланки 3 має місце сигнал DZ (збільшення положення регулювального органа турбіни). Ланка 3 представляє гідравлічний сервопривод зі сталою часу сервомотора Тс. У динамічному відношенні ланка 3 розглядається як інерційна першого порядку з передатною функцією:
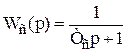 .
.
Еквівалентний статизм енергосистеми Sс (0,1 ¸ 0,15) значно перевищує статизм регуляторів окремих турбін (0,04 ¸ 0,05), тому що звичайно АРЧО на частині агрегатів не працює за різних причин (нечутливість, граничне навантаження та ін.). Стала часу Тсприймається рівною 0,25 або 0,5 с.
АРЧО, як показано було раніше, регулює частоту за статичним законом. При виникненні збурювання ΔРн частота (у відносних одиницях) у сталому режимі після дії АРЧО зміниться на величину:
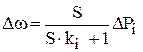 . (3.5)
. (3.5)
Ланка 5 відображає люфт МКТ (3,5%).
Ланка 6 - електродвигун МКТ. Стала часу двигуна приймається ТДВ = 0,25 с.
Ланка 7 з коефіцієнтом g визначає пропорційний, а ланки 8 і 9 формують інтегральний вплив АРЧМ з коефіцієнтом a. Функціональний перетворювач ФП у ланцюзі інтегрального впливу відображає нелінійну залежність навантаження даної електростанції від відносного приросту (зворотну ХВП). У роботі цю нелінійність можна не враховувати.
Якщо знехтувати впливом зворотного зв'язку за потужністю ΔРЭ , ланка з коефіцієнтом β виявляється включеним послідовно з ланками 7 і 9. Отже, добутки a×b і g×b є приблизно коефіцієнтами відповідно інтегрального і пропорційного впливу регулятора потужності.
Параметри a, b і g, що настроюються, підбираються таким чином, щоб забезпечувалася оптимальна якість регулювання частоти: при мінімальному часі регулювання, перерегулювання відсутнє або не перевищує 10% ¸ 20% [10].
Дослідження АРЧ і П виконується за допомогою програми IMDS (див. додатки А и Б).
3.2 Порядок виконання роботи
1. Скласти структурну схему моделювання АРЧ і П за допомогою пакета IMDS. Ланки 5, 8 можна не враховувати.
2. Використовуючи дані табл. 3.1 і рис. 3.4 скласти текст програми для структурної схеми АРЧ і П (при першому розрахунку прийняти α= 1 і γ = 0,01, що практично відповідає виключенню пропорційного впливу на систему регулювання).
3. В результаті моделювання на ЕОМ роботи тільки АРЧО за отриманим даними розрахувати перехідну характеристику Δω(t). По характеристиці визначити відхилення Dwу сталому режимі при первинному регулюванні і порівняти його з розрахованим за формулою (3.5).
4. Визначити коефіцієнта α і γ, що настроюються,за умовою забезпечення оптимальної якості регулювання частоти. Рекомендується при розрахунку на ЕОМ α і γзмінювати в межах:
при β = 0,1; α = 1; 2; 5; 10 і γ = 5; 10; 20; 50;
при β = 1; α = 0,5; 1; 2 і γ = 2; 5; 8; 10.
5. Дослідити вплив люфту МКТ на якість регулювання для одного з оптимальних значень α і γ.
Таблиця 3.1 - Вихідні дані для дослідження АСРЧ і П
| Номер варіанта | TJ, c | kH | Tп, c | S | ΔPH, о.е. |
| 1, 11 2, 12 3, 13 4, 14 5, 15 6, 16 7, 17 8, 18 9, 19 10, 20 | 1,8 1,9 2,0 2,1 2,2 1,8 1,9 2,0 2,1 2,2 | 0,2 0,25 0,28 0,3 0,25 0,3 0,28 0,25 0,23 0,2 | 0,1 0,1 0,12 0,12 0,14 0,14 0,14 0,1 0,1 0,12 | 0,01 0,02 0,01 0,02 0,01 0,02 0,01 0,02 0,01 0,02 |
Примітка до табл. 3.1 . Для варіантів 1 – 10 прийняти Тс =0,25 c і β = 0,1 а для варіантів 11 – 20 - Тс=0,5 c і β = 1.
3.3 Зміст звіту
1. Мета роботи.
2 Вихідні дані.
3. Структурна схема АСРЧ і П.
4. Структурна схема моделювання АСРЧ і П за допомогою пакета IMDS.
5. Програма і результати розрахунку.
6. Привести криві перехідного процесу для АРЧ і П у координатах α×β та γ×β і окремо - криві перехідного процесу при тільки первинному регулюванні частоти.
7. Аналіз отриманих результатів.
3.4 Контрольні питання
1. Поясните необхідність підтримки частоти в енергосистемі з високою точністю.
2. Які основні методи регулювання частоти в енергосистемі?
3. У чому полягає сутність первинного і вторинного регулювання?
4. Призначення регулятора частоти обертання турбіни.
5. Що таке регулюючий ефект навантаження?
6. Які вимоги пред'являються до показників якості регулювання частоти?
7. Як зміниться якість регулювання частоти при виключенні регулюючого впливу, пропорційного відхиленню частоти?
8. За якими критеріями може здійснюватися розподіл активної потужності станції між паралельно працюючими генераторами.
9. Функції регулятора частоти обертання турбіни.
10. Опишіть роботу АСРЧ і П за пропорційно - інтегральному відхиленню частоти за допомогою схеми на рис. 3.3.
11. Як здійснюється астатичне регулювання частоти статичним АРЧО?
12. Закон регулювання частоти і потужності має вигляд Δf + Sс×(Р - Рпр)=0. Укажіть особливості запису цього закону при статичному і астатичному регулюванні.
13. Як моделюється електрична система і парові турбіни?
14. Які задачі покладають на частотнорегулювані станції?
15. Які системи регулювання частоти і потужності використовуються для керування частотнорегулюваними станції.
16. Які допущення прийняті при моделюванні АСРЧ і П?
Лабораторна робота №4
АНАЛІЗ ПЕРЕХІДНИХ ПРОЦЕСІВ В ОБ'ЄДНАНІЙ ЕНЕРГОСИСТЕМІ ПРИ РЕГУЛЮВАННІ ЧАСТОТИ І ПЕРЕТІКАННЯ ПОТУЖНОСТІ
Мета роботи: оцінка динамічних властивостей автоматичної системи регулювання частоти і перетікання потужності в об'єднаній енергосистемі при різних значеннях настроювальних параметрів.
4.1 Основні відомості
В об'єднаній електроенергетичній системі (ОЕС) є декілька взаємно зв'язаних електроенергетичних систем (ЕЕС). У кожній з ЕЕС установлені АСРЧ і П зі статизмом за перетіканням потужності в лініях зв'язку [2], які забезпечують спільне регулювання частоти і перетікання потужності. Закон регулювання для кожної ЕЕС має вигляд:
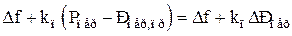 ,
,
де kп – коефіцієнт, що визначає відповідність регулюючих впливів,
Рпер,пр – запропоноване значення потужності перетікання.
Для кожної ЕЕС закон реалізується з урахуванням знака потужності перетікання. Реалізація цього закону регулювання може здійснюватися як за миттєвим відхиленням частоти і потужності, так і за інтегральною функцією.
Зміною коефіцієнта kп можна так настроїти АСРЧ і М кожної ЕЕС, щоб зміни навантаження в даної ЕЕС покривалися зміною потужності тільки її частотнорегульованими електростанціями. При цьому буде мати місце автономність ЕЕС. Таке настроювання досягається при коефіцієнті kп рівному коефіцієнту статизма даної ЕЕС.
Дослідження перехідних процесів пов'язаних з регулюванням перетікання потужності неможливо при приведенні енергосистеми до одного агрегату. Тому розглянемо систему, що складається із двох енергосистем у вигляді двох концентрованих частин, близьких або однакових за потужністю. Нехай частини цієї об'єднаної енергосистеми мають однакові номінальні потужності і однакові еквівалентні сталі механічної інерції TJ. Нехай також ці частини однаково навантажені, а перетікання між ними становить невелику частку їхньої потужності. Тоді можна в лінійному наближенні записати рівняння руху у відносних відхиленнях:
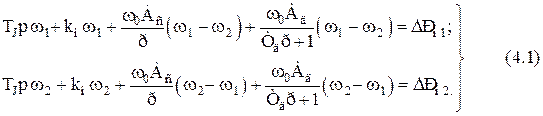
Другі члени кожного рядка відповідають місцевому навантаженню енергосистеми, що є функцією частоти. Треті члени - синхронної потужності, що віддається (одержується) по лінії, яка зв'язує частині об'єднаної енергосистеми між собою. Четверті члени визначають збільшення асинхронної потужності в кожній енергосистемі. Члени в правій частині рівняння представляють собою збурювання за навантаженням, що прийняті не залежними від частоти. Умова однакового завантаження ЕЕС дозволила прийняти в (4.1) рівність коефіцієнтів регулюючого ефекту навантаження kн,а відносно мала величина перетікання - рівність коефіцієнтів Аді Тд [10]. Всі величини в (4.1) віднесені до потужності частин об'єднаної енергосистеми.
Рівнянням (4.1) відповідає структурна схема на рис. 4.1, де:
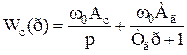 . (4.2)
. (4.2)
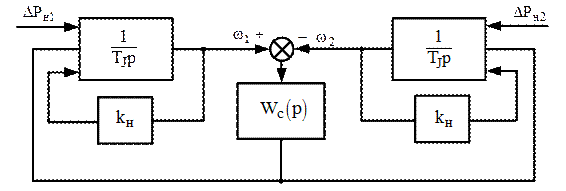
Рисунок 4.1 - Структурна схема нерегульованої об'єднаної енергосистеми
Рівняння (4.1) і схема на рис. 4.1 складені виходячи з припущення, що збурювання DРн у початковий момент сприймаються станціями тільки своєї енергосистеми. У випадку слабкого зв'язку між енергосистемами це практично відповідає дійсності, тому що збурювання спочатку розподіляється зворотно пропорційно реактивностям, що зв'язують точку прикладення збурювання з точками прикладання ЕРС. Однак іу всіх інших випадках похибка, що має місце тільки поблизу t=0, не істотна при аналізі процесів регулювання частоти і потужності. За незалежні змінні в (4.1) прийняті частоти w1 і w2 кожної із частин енергосистеми. Характеристичний визначник системи рівнянь (4.1) буде мати вигляд:
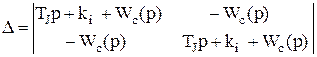 . (4.3)
. (4.3)
Він розкладається на два співмножника. З врахуванням цього характеристичне рівняння буде мати вигляд:
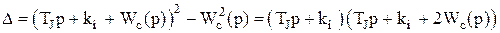 . (4.4)
. (4.4)
Кожний зі співмножників відповідає певному руху в об'єднаній енергосистемі, а умови стійкості можуть визначатися на основі розгляду кожного з них окремо. Щоб з'ясувати, з яким саме рухом зв'язаний кожний співмножник, вирішимо систему (4.1) відносно w1 і w2 при східчастому збурюванні DРн1 і запишемо операторні вирази величин (w1 - w2) і (w1+w2)/2:
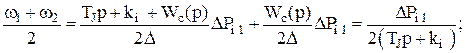 (4.5)
(4.5)
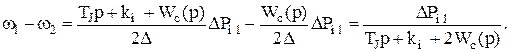 (4.6)
(4.6)
З (4.5) і (4.6) маємо, що перший співмножник характеристичного багаточлена (4.4) відноситься до зміни середньої частоти в об'єднаної енергосистеми, а другий - до зміни різниці частот двох енергосистем. Якщо помножити різницю частот на Wc(p),тоодержимо oпeраторний вираз зміни перетікання потужності між частинами об'єднаної енергосистеми:
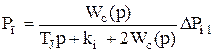 . (4.7)
. (4.7)
Вираз (4.5) відповідає перехідної характеристики у вигляді експоненти, що має при типових значеннях параметрів енергосистем (ТJ = 10 с, kн = 2) сталу часу 5 с. У вираз (4.6) замість Wc(p) підставимо (4.2):
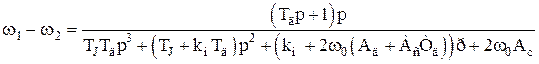 . (4.8)
. (4.8)
Знаменник виразу (4.8) при будь-яких реальних значеннях параметрів має один від’ємний і два комплексних сполучених корені, а різниця частот містить дві складові: аперіодичну (експоненціальну) і коливальну згасаючу, що прагне до нуля в часі і зменшується в міру посилення зв'язку частин об'єднаної енергосистеми (збільшення Асі Ад) [10]. Аперіодична складова практично при всіх значеннях параметрів залишається незначною. При досить сильному зв'язку різниця w1 - w2 стає дуже малою. При цьому практично залишається тільки одна змінна середня частота. Цей випадок був предметом розгляду при приведенні енергосистеми до одного агрегату (див. роботу №3). Коефіцієнт 2, що з'явився в (4.5), зв'язаний лише з тим, що величина збурювання DРН1 в (4.1) і наступних виразах віднесена до потужності кожної частини, тобто до половини потужності об'єднаної енергосистеми.
Відмовимося від рівності частин об'єднаної енергосистеми за потужністю, але збережемо рівність виражених у відносних одиницях параметрів TJі kн. Таке допущення близько до дійсності практично для всіх однорідних за составом частин об'єднаної енергосистеми (наприклад, тілько з теплових станцій або з однаковою питомою вагою ГЕС).
Для спільного рішення рівнянь (4.1) у цьому випадку необхідно прийняти однакове значення базисної потужності. Нехай це буде потужність першого району Р1. В результаті одержимо характеристичний визначник, що буде розкладатися на такі множники:
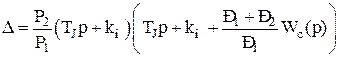 . (4.9)
. (4.9)
У цьому випадку також перший співмножник відповідає процесу зміни середньозваженого по потужності енергосистем значення частоти:
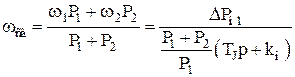 , (4.10)
, (4.10)
а другий, як і раніше, процесу зміни різниці частот:
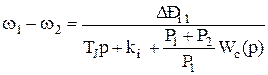 . (4.11)
. (4.11)
При P1 = P2вирази (4.9) - (4.11) перетвориться відповідно в (4.4) - (4.6).
Для регульованої об'єднаної енергосистеми в лівих частинах рівнянь (4.1) з'являться члени, що відповідають регулюючим впливам. Якщо ці впливи однакові в обох частинах енергосистеми, то система залишається симетричною, і характеристичний визначник по колишньому розкладається на два співмножника. Нехай регулювання здійснюється у функції тільки частоти (працюють тільки регулятори турбін, тобто АРЧО за миттєвим відхиленням), при цьому передатна функція регулятора:
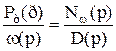 , (4.12)
, (4.12)
де Рт - потужність, що виробляється турбіною.
Якщо здійснюється спільне регулювання частоти і перетікання потужності, то в рівняння руху (4.1) необхідно включити впливи як за частотою, так і за перетіканням. Передатну функцію регулюючого впливу за перетіканням позначимо:
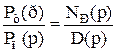 . (4.13)
. (4.13)
На рис. 4.2 наведена структурна схема об'єднаної енергосистеми з регулюванням по частоті і перетіканню потужності.
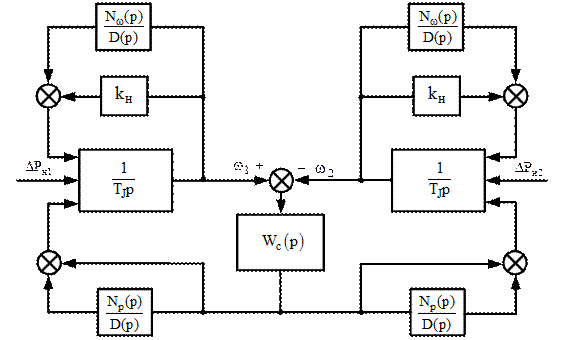
Рисунок 4.2 - Структурна схема об'єднаної енергосистеми з регулюванням частоти і перетікання потужності
У загальному випадку , знаменники виразів (4.12) і (4.13) можуть розрізнятися. Однак, оскільки регулюючі впливи і за частотою і за перетіканням діють в одному і тому же ланцюгу ланок (МКТ, турбіна і т.д.), то шляхом відповідної зміни чисельників легко зробити знаменники однаковими.
Після простих, аналогічних, що виконувалися раніше перетворень, можна також одержати характеристичний визначник. Він розкладається також на два співмножники.
Перший співмножник цього характеристичного визначника не змінився в порівнянні з попередніми співвідношеннями, тобто стійкість процесу регулювання середньої частоти виявляється не залежної від регулюючого впливу за перетіканням. Другий співмножник характеризує регулювання різниці частот регулятором за передатною функцією:
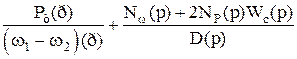 . (4.14)
. (4.14)
Якщо ж урахувати зв'язок між різницею частот і зміною перетікання , то другий співмножник буде характеризувати регулювання перетікання регулятором з передатною функцією:
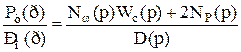 . (4.15)
. (4.15)
Рівняння (4.14) і (4.15) порівняємо з рівняннями (4.12) і (4.13). Очевидно, що в той час як вплив за перетіканням не впливає на стійкість регулювання частоти, зворотне твердження не відповідало б дійсності, тому що в (4.15) входять оператори впливу як за перетіканням NP(p), так і за частотою Nw(p).
В нерегульованій об'єднаній енергосистемі зміна середньої частоти протікає за експоненціальним законом зі сталою часу TJ/kН, а зміна різниці частот містить дві прагнучі до нуля складові: експоненціальну і коливальну. Період коливань у більшості, випадків близький до 1 с. Регулятор частоти на них реагувати не буде, так само як регулятор потужності не реагує на коливальну складову потужності генератора (див. § 5-2 в [10]). Стала часу експоненціальної складової незначна за величиною і близька до сталої часу зміни середньої частоти. Однак на відміну від зміни середньої частоти різниця частот прагне до нуля. Таким чином, «система регулювання різниці частот» відрізняється від «системи регулювання середньої частоти» заміною інерційної ланки реальною ланкою, що диференціює, з дуже невеликим коефіцієнтом передавання. Якщо стійка друга систему, то тим більше буде стійка перша. Отже, буде стійка і у цілому система регулювання частоти в об’єднаної енергосистемі. Остаточний вивід полягає в тім, що система регулювання частоти, стійка в концентрованій енергосистемі, буде стійка і у симетричній енергосистемі з двох частин. Міркуючи так само, як у випадку рівнянь (4.9) ¸ (4.11), можна поширити цей вивід на випадок як двох нерівних по потужності частин, так, очевидно, і на випадок довільного числа частин.
Слід зазначити, що аналітичний аналіз не виявляє якої-небудь нестійкості, пов'язаної з використанням в обох частинах енергосистеми астатичного регулювання частоти за миттєвим відхиленням. Якщо характеристичне рівняння Ww(p) = 0 відповідає стійкому регулюванню в одній із частин енергосистеми, то принаймні при певних значеннях вхідних в Wc(p) параметрів буде стійким і загальний рух. Цим доводиться, що відоме в експлуатації явище нестійкості паралельної роботи астатичних регуляторів має іншу природу: воно зв'язано не зі структурою і співвідношенням параметрів системи регулювання, а з нелінійними ефектами ( розходженням величин зон нечутливості, різними коефіцієнтами підсилення при наявності зон нечутливості і нестабільністю (розбіжністю) уставок регуляторів). Відповідно і нестійкість проявляється не у вигляді розбіжних коливань або аперіодичного наростання координат, а у вигляді поступової розбіжності потужностей, що генеруються регулюючими електричними станціями, у цьому випадку - частинами енергосистеми. Отже, стійкість може бути забезпечена без зміни структури і параметрів шляхом застосування регуляторів без зони нечутливості і з високою точністю і стабільністю настроювання.
Наведене моделювання об'єднаної енергосистеми засновано на оцінці характеристик асинхронної потужності (параметрів АД, ТД). На відміну від випадку роботи генератора на шини незмінної напруги в розглянутому випадку є три незалежні змінні d12, Eq1і Eq2,тому збільшення потужності, що генерується у кожній частині об'єднаної енергосистеми, можна записати у вигляді:
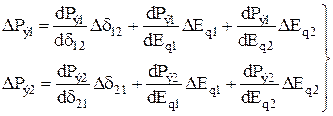
Члени виду 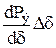 представляють собою прирощення синхронної потужності. Члени, у які входять прирощення ЕРС Eq, щовиникають при взаємному ковзанні частин енергосистеми, відповідають асинхронній потужності.
представляють собою прирощення синхронної потужності. Члени, у які входять прирощення ЕРС Eq, щовиникають при взаємному ковзанні частин енергосистеми, відповідають асинхронній потужності.
Розрахунок перехідних характеристик системи АСРЧ і М за миттєвим відхиленням виконується для структурної схеми АСР зображеної на рис. 4.3
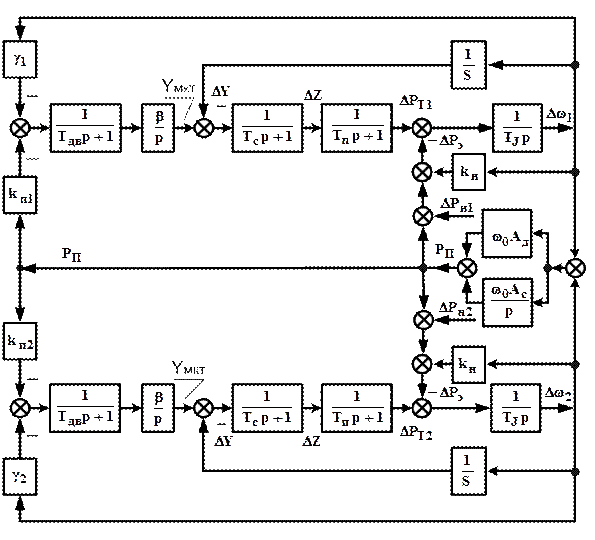
Рисунок 4.3 - Структурна схема регулювання частоти і перетікання потужності за миттєвим відхиленням в об'єднаній енергосистемі
На рис. 4.3 кожна з однакових частин енергосистеми приведена до одного парового турбоагрегату без проміжного перегріву. Для зручності порівняння з іншими схемами і розрахунковими випадками коефіцієнт передачі МКТ позначений окремою величиною b. Він при розрахунках приймається рівним одиниці. Сталі часу ТДВ і ТС приймаються такими ж як і в лабораторній роботі №3. Коефіцієнт синхронної потужності w0АС = 30, тобто АС » 0,1. Коефіцієнт асинхронної потужності АДзадається в кожному варіанті розрахунку. В якості збурювання розглядається східчаста зміна навантаження DРН в одній із частин енергосистеми. За одиницю прийнята потужність однієї частини об'єднаної енергосистеми.
4.2 Завдання
1. Скласти структурну схему моделювання системи регулювання частоти і перетікання потужності за миттєвим відхиленням за допомогою програми IMDS.
2. Скласти текст програми для розрахунку системи регулювання частоти і перетікання потужності з урахуванням симетричності обох частин об'єднаної енергосистеми і вихідних даних, наведених у табл. 4.1.
3. Виконати розрахунок на ЕОМ перехідних характеристик Dw1(t), Dw2(t) і Рп(t) нерегульовані об'єднані енергосистеми при g1=g2=0, kп1= kп2=0, w0Ад=1 і при східчастій зміні тільки DРн1 (DРн2=0). Регулювання в цьому випадку здійснюється статичним регулятором частоти обертання АРЧО. Сталі значення відхилення частоти і перетікання потужності визначаються за співвідношеннями:
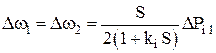 и.
и. 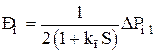
За допомогою перехідних характеристик визначити сталі значення Dw1(t), Dw2(t) і Рп(t) і зрівняти їх з результатами розраховані за зазначеними співвідношеннями.
4. Розрахувати на ЕОМ перехідні характеристики об'єднаної енергосистеми, коли регулювання частоти здійснюється тільки в першій її частині (g1=8 і g2=0, kп1= kп1=0) при східчастому прирощені потужності в другій частині DРн2 ( при цьому DРн1=0).
Визначити при якому значенні коефіцієнта асинхронної потужності зникає коливальна складова перехідного процесу в першій і другій частинах об'єднаної енергосистеми Dw1(t), Dw2(t). Рекомендується змінювати w0Ад від 0 до 10.
5. Виконати розрахунок на ЕОМ перехідні характеристики Dw1(t), Dw2(t) і Рп(t) при регулюванні в обох частинах об'єднаної енергосистеми за законом Uрег=g×w+ kп×Рп при східчастій зміні тільки DРн2 (DРн1=0). Рекомендується змінювати g і kп у наступних межах: g = 1; 4; 6; 12 і kп=0,05; 0,1; 0,2; 0,5; 0,8; 1,0. Параметри регулятора g і kп установлюються однаковими в обох частинах енергосистеми. Значення w0Ад приймається за результатами розрахунків у пункті №4 (мінімальне значення, що відповідає зникненню коливального характеру перехідної характеристики Dw1(t) або Dw2(t)).
6. Виконати розрахунки на ЕОМ перехідних характеристик системи регулювання частоти і перетікання потужності з різним настроюванням регулятора: g1=2, kп1=0,33 і g2=0,5, kп2=0,083. У першому опиті задається збурювання в першій частині об'єднаної енергосистеми DРн1 (DРн2=0), а в другому опиті в другій її частині DРн2 (DРн1=0).
Таблиця 4.1 - Дані для дослідження АСР частоти і перетікання потужності
| Номер варіанта | TJ, c | b | KH | Tп, с | S | ΔPH,о.е. |
| 1, 11 2, 12 3, 13 4, 14 5, 15 6, 16 7, 17 8, 18 9, 19 10, 20 | 1,8 1,9 2,0 2,1 2,2 1,8 1,9 2,0 2,1 2,2 | 0,2 0,25 0,28 0,3 0,25 0,3 0,28 0,25 0,23 0,2 | 0,1 0,1 0,12 0,12 0,14 0,14 0,14 0,1 0,1 0,12 | 0,04 0,06 0,08 0,04 0,06 0,08 0,04 0,06 0,08 0,07 |
Примітка до табл. 4.1. Для варіантів 1 – 10 прийняти Тс =0,25 с, а для варіантів 11 – 20 вибрати Тс=0,5 с.
4.3 Зміст звіту
1. Мета роботи.
2. Вихідні дані.
3. Структурна схема автоматичної системи регулювання частоти і потужності перетікання.
4. Структурна схема моделювання системи регулювання за допомогою програми IMDS.
5.. Програма і результати розрахунку.
6. Криві перехідного процесу. Для розрахунків відповідно до пункту 5 завдання показати їх у координатах kп і γ.
7. Аналіз отриманих результатів.
4.4 Контрольні питання
1. При яких умовах у лінії зв'язку з'явиться перетікання потужності і куди воно буде спрямовано?
2. Поясните термін «обмінна потужність» енергосистеми.
3. Від чого залежить синхронна і асинхронна потужність енергосистеми?
4. Які види руху визначає характеристичний визначник симетричної об'єднаної енергосистеми?
5. Як змінюється вид перехідної характеристики Dw(t) = Dw1(t) - Dw2(t) при посиленні зв'язку частин об'єднаної енергосистеми?
6. Який тип регулювання буде якщо в об'єднаній енергосистемі де діють тільки регулятори частоти обертання турбін?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|