Пример 82. Построить условную развертку сферы (рис. 311).

Пример 82. Построить условную развертку сферы (рис. 311).

Строим фронтально проецирующий цилиндр, огибающий сферу по главному меридиану. Двумя горизонтально проецирующими плоскостями, проходящими через ось сферы, вырезаем из нее и цилиндра “лепесток”, симметричный относительно главного меридиана сферы. Поверхность сферического "лепестка" заменяем поверхностью цилиндрического "лепестка" и строим развертку последнего. Цилиндрический “лепесток” аппроксимируем гранной поверхностью. Для этого линию соприкасания сферы с цилиндром в пределах "лепестка" поделим на некоторое количество равных частей и соединим их хордами. Через полученные точки А, B,…проведем горизонтальные секущие плоскости уровня. Они будут пересекать "лепесток" по отрезкам образующих цилиндра A11A21, B11B21,…Таким образом, элементами цилиндрического "лепестка" будут пространственные равнобочные трапеции. Рассмотрим одну из них, например, трапецию A1A2B1B2. Ее основаниями являются отрезки образующих обвертывающего цилиндра, которые проецируются в истинную величину на горизонтальную плоскость проекций (A11A21 и B11B21). Высота трапеции равна величине хорды главного меридиана сферы. Аналогично определяются сторон других входящих в данный “лепесток» трапеций. Условная развертка поверхности сферы будет представлять собой совокупность разверток всех "лепестков".

Пример 83. Построить условную развертку поверхности вращения (рис.312).

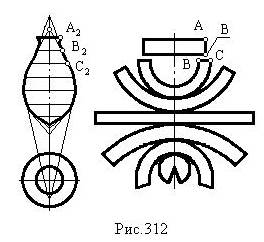
Семейством горизонтальных плоскостей уровня рассечем заданную поверхность на семь “поясов” (будем считать, что выбранного количества “поясов” достаточно для обеспечения заданной точности построения развертки). Первый и четвертый из них аппроксимируем отсеками цилиндров, а все остальные – конусами (при этом второй, третий, пятый и шестой “пояса” – усеченными).

Известно, что точной разверткой прямого кругового цилиндра будет прямоугольник с высотой, равной высоте цилиндра, и шириной, равной 2pR, где R - радиус окружности основания цилиндра. В данном случае высотами цилиндров будут высоты упомянутых "поясов", а радиусами окружностей оснований - радиусы соответствующих параллелей.

Заметим, что для построения развертки усеченного конуса достаточно построить развертки конусов с основаниями, равными нижнему и верхнему основаниям “пояса”. При этом напомним, что точной разверткой прямого кругового конуса является сектор окружности радиусом, равным длине его образующей l и углом при вершине a = 360°R/l, где R - радиус окружности основания конуса.

⇐ Предыдущая 1 2 3 45