Пример 81. Построить условную развертку поверхности купола (рис.309).

Пример 81. Построить условную развертку поверхности купола (рис.309).

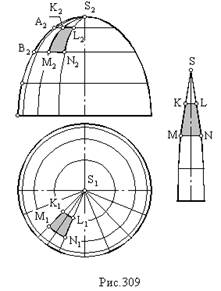
Аппроксимировать заданную поверхность можно отсеками плоскостей. Для этого заданную поверхность необходимо рассечь достаточным количеством меридиональных и горизонтальных плоскостей уровня. Условимся, что для достижения заданной точности построения достаточно разбить заданную поверхность меридиональными плоскостями на шестнадцать одинаковых “лепестков” и горизонтальными плоскостями уровня на четыре “пояса”. При этом в верхнем поясе образуются пространственные равнобедренные треугольники, а в остальных – пространственные равнобочные трапеции.

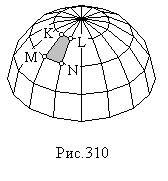
Рассмотрим, например, трапецию KLMN. Ее стороны KL и MN являются частями соответствующих параллелей, а стороны KM и LN – частями соответствующих меридианов. Если ее криволинейные стороны заменить отрезками прямых, то мы получим плоскую равнобочную трапецию. Основания этой трапеции являются хордами соответствующих параллелей, а боковые стороны – хордами соответствующих меридианов (рис.310). Хорды параллелей проецируются в истинную величину на горизонтальную плоскость проекций (K1L1 и M1N1), а истинная величина боковых сторон равна истинной величине хорд фронтального меридиана (K2M2 = L2N2 = A2B2). Аналогично определяются стороны остальных трапеций и треугольников, входящих в данный “лепесток” и строится его развертка. Совокупность разверток всех лепестков и дает условную развертку поверхности.

В ряде случаев поверхности вращения целесообразно аппроксимировать отсеками конусов и цилиндров.

⇐ Предыдущая 1 2 345 Следующая ⇒