Гиперболический параболоид

Гиперболический параболоид

Каноническое уравнение гиперболического параболоида 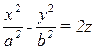(4).

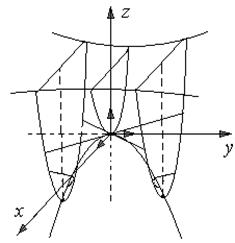
Свойства.

1.Поверхность симметрична относительно плоскости (xOz) и (уOz), оси Oz и начала координат.

Начало координат – это вершина гиперболического параболоида.

2.Точки пересечения с координатными осями.

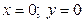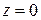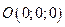→ → – вершина гиперболического параболоида.

3.Пересечения с координатными плоскостями и им параллельными.

1) Пусть гиперболический параболоид рассечен плоскостями, параллельными (xOz): .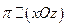

→ →

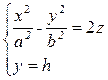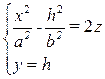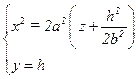
Первое уравнение системы – это уравнение параболы с осью, параллельной оси Оz, лежащей в плоскости у = h .

Аналогичные сечения получаются при пересечении гиперболического параболоида плоскостями, параллельными плоскости (yOz), т. е. х = h.

Если h = 0 = х, то .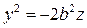

2) Пусть гиперболический параболоид рассечен плоскостями, параллельными (хOу)

→

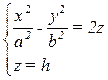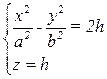
a. Если h < 0, то 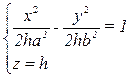– гипербола с действительной осью Oy, лежащая в плоскости z = h;

b. Если h = 0, то 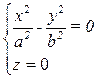– две пересекающиеся прямые, лежащие в плоскости z = 0, т. е. (хOу);

c. Если h > 0, то 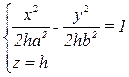– гипербола с действительной осью Ох.