
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Эллипсоид
Рассмотрим в пространстве плоскость 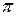 и некоторое действительное число
и некоторое действительное число 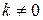 .
.
Определение. Отображение точек пространство по закону 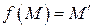 такое, что
такое, что 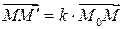 , где М0 – ортогональная проекция точки М на плоскость
, где М0 – ортогональная проекция точки М на плоскость 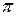 , есть преобразование пространства, называемое сжатием пространства к плоскости
, есть преобразование пространства, называемое сжатием пространства к плоскости 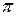 .
.
Рассмотрим k > 0, сжатие пространства к плоскости (xOy).
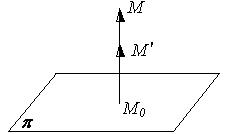
Пусть в репере 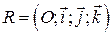 точки имеют координаты
точки имеют координаты 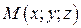 и
и 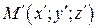 →
→ 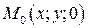 ,
, 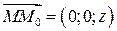 ,
, 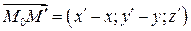
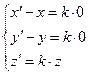 →
→ 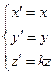 – формулы сжатия к плоскости (xOy).
– формулы сжатия к плоскости (xOy).
Аналогично получаются формулы сжатия к другим координатным плоскостям:
к (yOz) 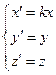 к (xOz)
к (xOz) 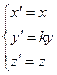
Эллипсоид
Рассмотрим эллипсоид вращения вокруг оси Oz 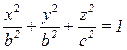 .
.
Рассмотрим поверхность, полученную из нее сжатием пространства к плоскости, проходящей через ось вращения, а именно к плоскости (уOz) с коэффициентом 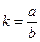 , где а > 0.
, где а > 0.
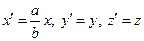 →
→ 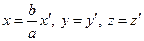
Получим каноническое уравнение трехостного эллипсоида 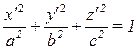 или
или 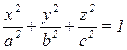 (1).
(1).
Свойства.
1.Из (1) → 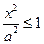 →
→ 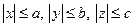 .
.
Т. е. все точки эллипсоида будут лежать внутри прямоугольного параллелепипеда с измерениями 2а, 2в, 2с.
2.Если точка 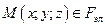 , то ей принадлежат точки
, то ей принадлежат точки 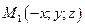 ,
, 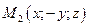 ,
, 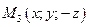 ,
, 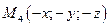 → тело симметрично относительно координатных плоскостей и начала координат.
→ тело симметрично относительно координатных плоскостей и начала координат.
Начало координат – это центр симметрии эллипсоида, называемый центром эллипсоида.
3.Точки пересечения с координатными осями.
Ох: 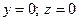 →
→ 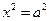 →
→ 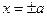 →
→ 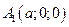 и
и 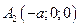
Оу: 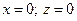 →
→ 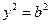 →
→ 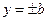 →
→ 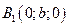 и
и 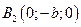
Оz: 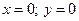 →
→ 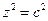 →
→ 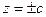 →
→ 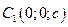 и
и 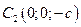
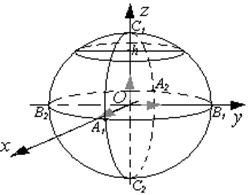
Эти точки называются вершинами эллипсоида
4.Пересечения с координатными плоскостями и им параллельными.
Пусть эллипсоид рассечен плоскостью, параллельной плоскости (xOy), т. е. 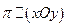 , значит, уравнение плоскости π: z = h. Таким образом, рассмотрим систему уравнений:
, значит, уравнение плоскости π: z = h. Таким образом, рассмотрим систему уравнений: 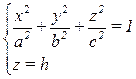 →
→ 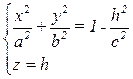
a. Если h = 0, то 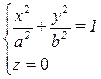 – эллипс с полуосями а, b, лежащий в плоскости (xOy);
– эллипс с полуосями а, b, лежащий в плоскости (xOy);
b. Если 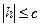 , то
, то 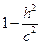 > 0 →
> 0 → 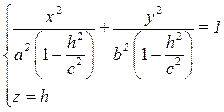 – эллипс, лежащий в плоскости z = h;
– эллипс, лежащий в плоскости z = h;
c. Если 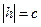 , то
, то 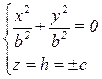 →
→ 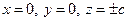 ,
,
т. е. имеем 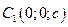 и
и 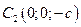 – две точки;
– две точки;
d. Если 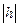 > с, то
> с, то 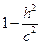 < 0 →
< 0 →
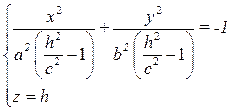 – мнимый эллипс
– мнимый эллипс
Аналогичные сечения получаются при пересечении эллипсоида плоскостями, параллельными плоскостям (xOz) и (yOz).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|