
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Двуполостный гиперболоид. Параболоид эллиптический
Двуполостный гиперболоид
Это поверхность, полученная из двуполостного гиперболоида вращения 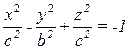 сжатием пространства к плоскости, проходящей через ось вращения, а именно к плоскости (уOz) с коэффициентом
сжатием пространства к плоскости, проходящей через ось вращения, а именно к плоскости (уOz) с коэффициентом 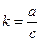 .
.
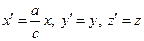 →
→ 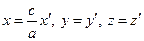
Получим каноническое уравнение двуполостного гиперболоида c осью Оу 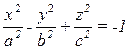 (3).
(3).
Свойства.
1.Поверхность симметрична относительно координатных плоскостей, осей координат, начала координат.
Начало координат – это центр двуполостного гиперболоида.
2.Точки пересечения с координатными осями.
Ох: 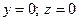 →
→ 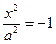 → Ø → не пересекает ось Oz
→ Ø → не пересекает ось Oz
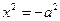 →
→ 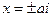 → Ох, Oz – мнимые оси;
→ Ох, Oz – мнимые оси;
Оу: 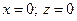 →
→ 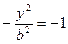 →
→ 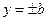 →
→ 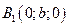 и
и 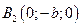 – вершины
– вершины
3.Пересечения с координатными плоскостями и им параллельными.
1) Пусть двуполостный гиперболоид рассечен плоскостями, параллельными (xOz): 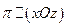 .
.
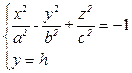 →
→ 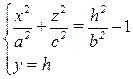
a. Если h = 0, то 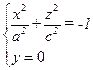 – мнимый эллипс, лежащий в плоскости (xOz);
– мнимый эллипс, лежащий в плоскости (xOz);
b. Если 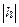 < b, то
< b, то 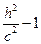 < 0
< 0
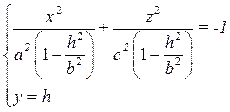 → мнимый эллипс;
→ мнимый эллипс;
c. Если 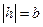 , то
, то 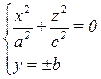 →
→ 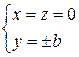 →
→ 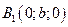 и
и 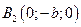 – вершины;
– вершины;
d. Если 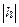 > b, то
> b, то 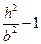 > 0 →
> 0 →
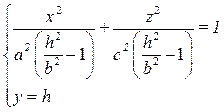 – эллипс;
– эллипс;
2) Пусть двуполостный гиперболоид рассечен плоскостями, параллельными (уOz)
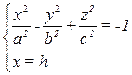 →
→ 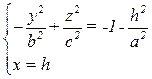 →
→ 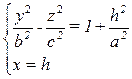
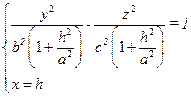 – гипербола с осью Оу.
– гипербола с осью Оу.
3) Аналогично получаются сечения двуполостного гиперболоида плоскостями, параллельными плоскости (хOу).
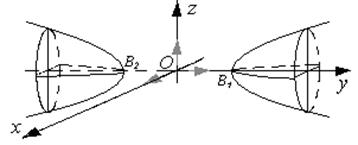
Параболоид эллиптический
Это поверхность, полученная из параболоида вращения 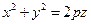 (p > 0) сжатием пространства к плоскости, проходящей через ось вращения.
(p > 0) сжатием пространства к плоскости, проходящей через ось вращения.
Пусть р = b, рассмотрим сжатие пространства к плоскости (уOz) с коэффициентом 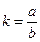 , где а > 0.
, где а > 0.
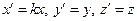 →
→ 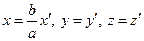
Получим каноническое уравнение эллиптического параболоида 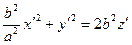 или
или 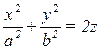 (4).
(4).
Свойства.
1.Если точка 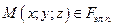 , то ей принадлежат точки
, то ей принадлежат точки 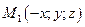 ,
, 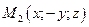 ,
, 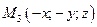 → тело симметрично относительно плоскостей (yOz), (xOz) и оси Oz.
→ тело симметрично относительно плоскостей (yOz), (xOz) и оси Oz.
Oz – ось эллиптического параболоида.
2.Точки пересечения с координатными осями.
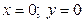 →
→ 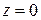 →
→ 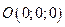 – вершина параболоида.
– вершина параболоида.
3.Пересечения с координатными плоскостями и им параллельными.
1) Пусть эллипсоид рассечен плоскостью, параллельной (xOy): 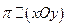
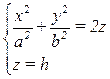 →
→ 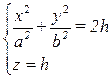
a. Если h < 0, то – мнимый эллипс;
b. Если h = 0, то 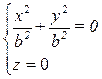 →
→ 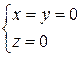 → вершина
→ вершина 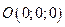 ;
;
c. Если h > 0, то 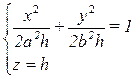 – эллипс.
– эллипс.
2) Пусть эллипсоид рассечен плоскостью, параллельной (xOz):
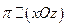
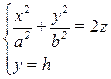 →
→ 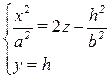 →
→ 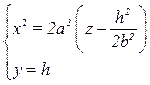 – парабола с осью Oz;
– парабола с осью Oz;
Если h = 0, то 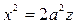 .
.
3) Аналогичные сечения получаются при пересечении эллипсоида плоскостями, параллельными плоскости (yOz).
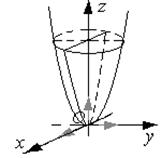
Параболоид эллиптический можно получить другим способом.
Заставим параболу 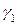 бегать по параболе
бегать по параболе 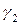 . Эти параболы возьмем так, чтобы они имели общую вершину в начале координат и лежали в двух взаимно перпендикулярных плоскостях (хOz) и (yOz).
. Эти параболы возьмем так, чтобы они имели общую вершину в начале координат и лежали в двух взаимно перпендикулярных плоскостях (хOz) и (yOz).
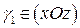 :
: 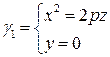
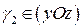 :
: 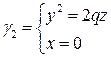
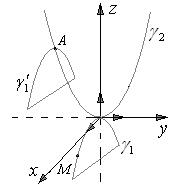
Пусть парабола 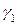 переместилась в точку
переместилась в точку 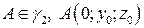 .
.
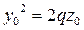 (1)
(1)
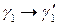 :
: 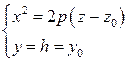 (2)
(2)
Из (1) выразим 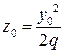 и подставим в (2) →
и подставим в (2) →
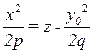 или
или 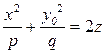 .
.
Если плоскость 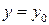 будет пробегать все действительные значения, то любая точка
будет пробегать все действительные значения, то любая точка 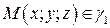 будет описывать поверхность, заданную уравнением
будет описывать поверхность, заданную уравнением
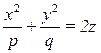 (3)
(3)
Возможны случаи:
1. р > 0, q > 0 → 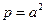 ,
, 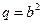 →
→ 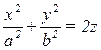 – уравнение эллиптического параболоида с осью Оz,
– уравнение эллиптического параболоида с осью Оz,
2. р > 0, q < 0 → 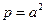 ,
, 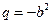 →
→ 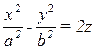 (4) – уравнение гиперболического параболоида.
(4) – уравнение гиперболического параболоида.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|