
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
эллиптический параболоид. гиперболический параболоид
7) эллиптический параболоид
Определение 7. Эллиптическим параболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением
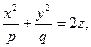 где
где 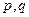 - параметры. (5)
- параметры. (5)
С помощью сечений исследуем эту поверхность:
1) 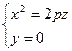 и
и 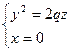 (16.3).
(16.3).
(В сечениях параболы: OZ – ось симметрии, O(0;0;0) – вершина)
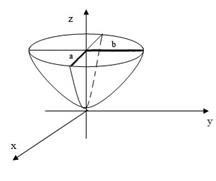 2)
2) 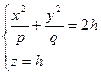
а) при h>0 сечения – эллипсы;
б) при h=0 плоскость z=0 касается параболоида (эллипс вырождается в точку);
в)при h<0 – мнимый эллипс.
Если p=q, эллиптический параболоид можно рассматривать, как поверхность, образованную вращением параболы вокруг ее оси (параболоид вращения).
8) гиперболический параболоид
Определение 8. Гиперболическим параболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением
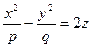 (p,q>0). (6)
(p,q>0). (6)
Установим геометрический вид поверхности:
Рассмотрим сечения:
1) 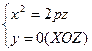 . В сечении парабола, OZ – ось симметрии, ветви направлены вверх, вершина – в начале координат.
. В сечении парабола, OZ – ось симметрии, ветви направлены вверх, вершина – в начале координат.
2) 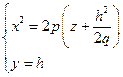 . В сечении – такие же (как в (1)) параболы
. В сечении – такие же (как в (1)) параболы 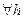 .
.
3) 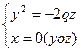 . В сечении парабола, OZ – ось симметрии, ветви направлены вниз, вершина – в начале координат.
. В сечении парабола, OZ – ось симметрии, ветви направлены вниз, вершина – в начале координат.
4) 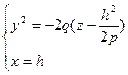 . В сечении
. В сечении 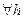 такие же параболы, как в (3).
такие же параболы, как в (3).
5) 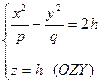 или
или 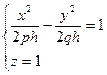 .
.
а) при h>0 в сечении гиперболы в плоскости OXZ;
б) при h<0 в сечении гиперболы в плоскости OYZ;
в) при h=0 в сечении гипербола вырождается в пару пересекающихся прямых.
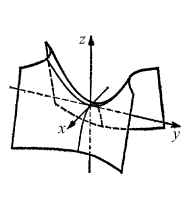
Таким образом имеем седлообразную поверхность. (0;0;0) – вершина, p,q – параметры.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|