однополостный гиперболоид. двуполостный гиперболоид

5) однополостный гиперболоид

Определение 5. Однополостным гиперболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

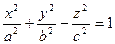. (3)

Установим его геометрический вид.

Рассмотрим сечения с координатными плоскостям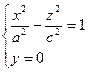и:

и 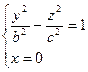(В сечениях получаются гиперболы)

Также рассмотрим сечения поверхности плоскостями :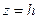

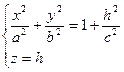а) 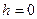, 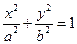- самый маленький эллипс.

б) , .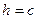

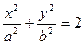в) , .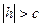

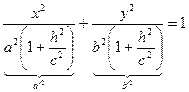Заметим, если 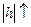, то .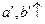

г) если 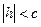, , 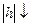то .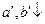

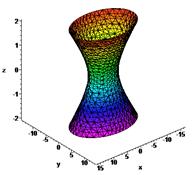
Таким образом, рассмотренные сечения позволяют изобразить однополостный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления. 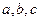– полуоси (чтобы изобразить 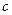, следует построить основной прямоугольник какой-нибудь из гипербол).

6) двуполостный гиперболоид

Определение 6. Двуполостным гиперболоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

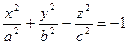. (4)

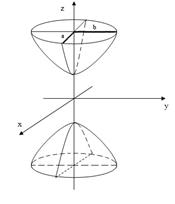С помощью аналогичного исследования нетрудно установить вид поверхности. В сечениях плоскости oXZ (y=o) и oYZ (x=0) получаются гиперболы

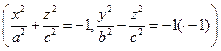При сечениях z=h:

а) при 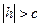плоскость пересекает поверхность по эллипсу;

б) при 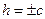плоскости 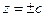касаются поверхности в точках (0;0; );

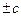в) при 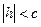точек пересечения плоскости 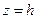с поверхностью не существует (мнимый эллипс).

Итак, двуполостный гиперболоид состоит из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши.

⇐ Предыдущая 1 234 Следующая ⇒