Контакты

Случайная статья

Конические поверхности. II тип задач. по виду уравнения определяются свойства поверхности). эллипсоид

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

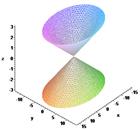
3) Конические поверхности

Определение 3.Поверхность, образованная прямыми, пересекающимися в одной точке и проходящими через каждую точку линии 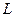- называется конической поверхностью.

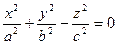
II тип задач

(по виду уравнения определяются свойства поверхности)

Основным методом решения таких задач является метод сечений, который заключается в поиске линий пересечений данной поверхности плоскостями, параллельными координатным плоскостям.

4) эллипсоид

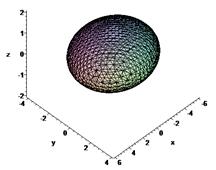
Определение 4. Эллипсоидом называется поверхность, которая в прямоугольной системе координат определяется уравнением

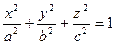. (2)

Установим геометрический вид эллипсоида.

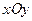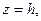
Рассмотрим сечения эллипсоида плоскостями параллельными плоскости ( 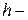любое число).

Линия сечения определяется системой:

(**)

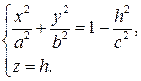
Исследуем (**).

а) 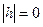, тогда 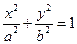– эллипс в плоскости , причем самый большой.

б) 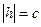, тогда 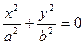– линия (**) вырождается в точки .

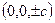(плоскости 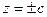касаются эллипсоида)

в) 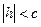, тогда .

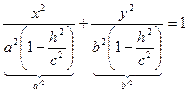Таким образом, плоскость 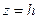пересекает эллипсоид по эллипсу, причем, если 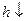, то 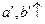, поэтому при 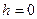, получается самый большой эллипс.

г) 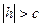, то 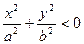- мнимый эллипс, точек пересечения с 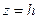не .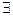

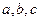- полуоси эллипсоида. Если 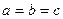, то эллипсоид является сферой.

Аналогично рассматриваются сечения, если 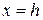или .

⇐ Предыдущая 123 4 Следующая ⇒

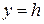© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.