Решение задания 2.1

⇐ ПредыдущаяСтр 4 из 7Следующая ⇒

Решение задания 2.1

Студент – = Чернавин Денис Леонидович.

«Ч» - 0х 0427 – 0000 0100 0010 0111– N_Ф1=5.

«е» - 0х 0435 – 0000 0100 0011 0101 – N_Ф2=5.

N_Ф1+N_Ф2= 10 - выбираем четную последовательность прямоугольных импульсов.

«б» - 0х0431 –0000 0100 0011 0001– N_ф3=4, U=4 B;

«С» - 0x041B – 0000 0100 0001 1011–N_o₁=5, Q=5.

В фамилии 8 букв, следовательно, Т=8 мс. При Q=5, длительность импульса τ_и в три раза меньше периода Т.

Для рассматриваемого варианта временная реализация будет иметь вид:

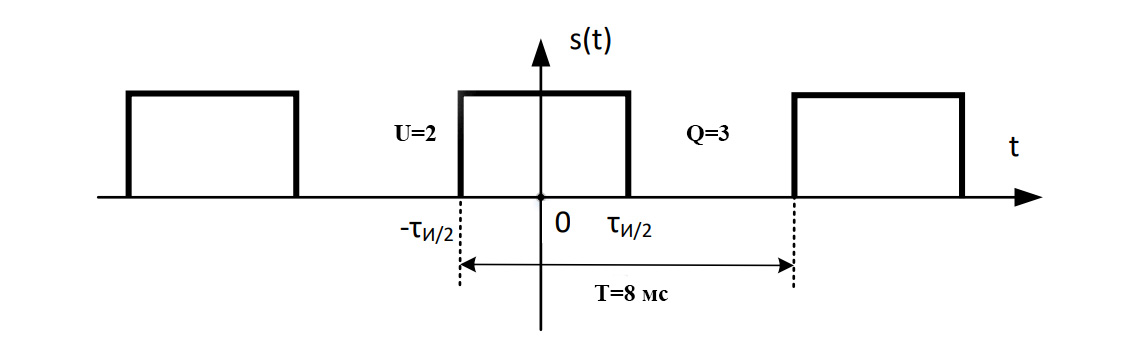
Рис.7 Временная реализация в соответсвии с заданием.

Определим коэффициенты ряда Фурье.

Среднее значение или постоянная составляющая сигнала:

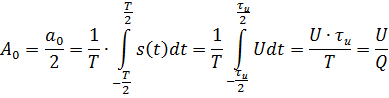
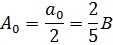
Рассчитываем коэффициенты a_n и b_n:

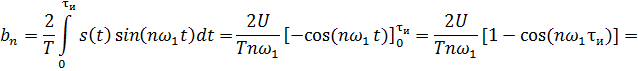
Вычислим среднюю мощность за период последовательность прямоугольных импульсов по временной реализации:

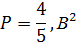
Определим мощность постоянной составляющей:

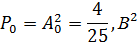
Определим мощности n-ых гармоник:

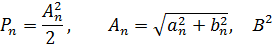
Определим начальные фазы n-ых гармоник:

𝜑_𝑛=𝑎𝑟𝑐𝑡𝑔 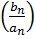, рад

n
Частота n/T, Гц
А₀, В	0.4
a_n, B	0.6055	0.1871	-0.1247	-0.1514		0.1009	0.0535	-0.0468	-0.0673
b_n, B	0.4399	0.5758	0.3839	0.1100		0.0733	0.1645	0.1440	0.0489
A_n, B	0.7484	0.6055	0.4036	0.1871		0.1247	0.1730	0.1514	0.0832
φ_n, рад	0.6283	1.2566	1.8850	2.5133	3.1416	0.6283	1.2566	1.8850	2.5133
P, B²	0.8
P₀, B²	0.16
P_n, B²	0.2800	0.1833	0.0815	0.0175		0.0078	0.0150	0.0115	0.0035

Результаты расчетов сводим в таблицу:

Таблица 2.1

Теперь для проверки правильности найденных нами коэффицинтов и мощностей воспользуемся программой MatLab. Коды будут следующими:

% расчёт коэффициентов без нулевого индекса

U=2; % амплитуда

Q=5; % скважность

n1=[1 2 3 4 5 6 7 8]; % массив индексов от 1 до 8

an=((U/pi)./n1).*sin((2*pi/Q)*n1); % расчёт коэффициентов an

bn=((U/pi)./n1).*(1-cos((2*pi/Q)*n1)); % расчёт коэффициентов bn

An=sqrt(an.^2+bn.^2); % расчёт коэффициентов Аn

fin= atan2(bn, an); % расчёт начальных фаз φn

Pn=(An.^2)/2; % расчёт мощностей гармоник Рn

% добавляем коэффициенты с нулевым индексом

n=[0 n1]; % массив индексов с учётом нулевого (от 0 до 8)

A0= U/Q; % постоянная составляющая, гармоника с индексом 0

P0= A0^2; % мощность постоянной составляющей

an=[A0 an]; % массив коэффициентов an с учётом нулевого

An=[A0 An]; % массив коэффициентов Аn с учётом нулевого

bn=[0 bn]; % массив коэффициентов bn с учётом нулевого

fin=[0 fin]; % массив коэффициентов φn с учётом нулевого

Pn=[P0 Pn]; % массив коэффициентов Рn с учётом нулевого

stem(n, An)

Расчет коэффициентов a_n ряда Фурье:

% выводим графики (показан для коэффициентов an)

stem(n, an)

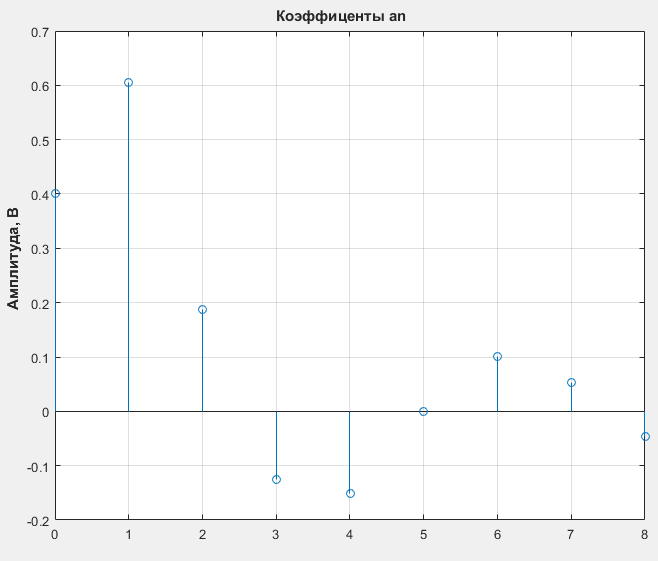
Рис.8 Коэффициенты a_n

Расчет коэффициентов b_n ряда Фурье

% выводим графики (показан для коэффициентов b_n)

stem(n, b_n)

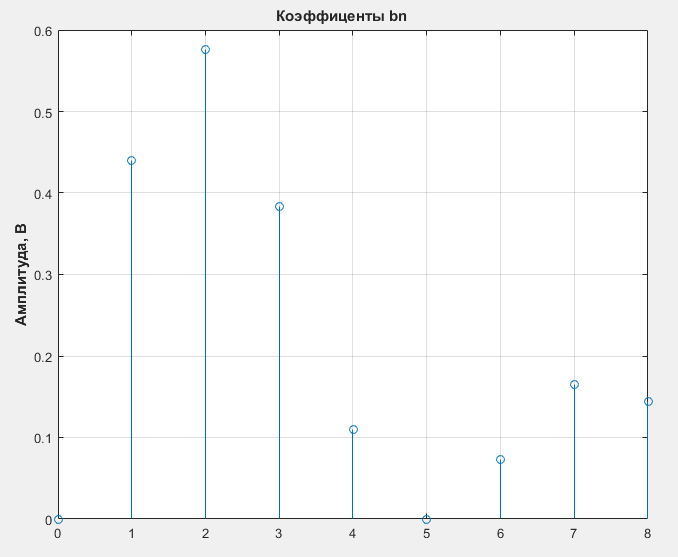
Рис.9 Коэффциенты b_n

Расчет амплитуд гармоник:

% выводим графики (показан для коэффициентов An)

stem(n, An)

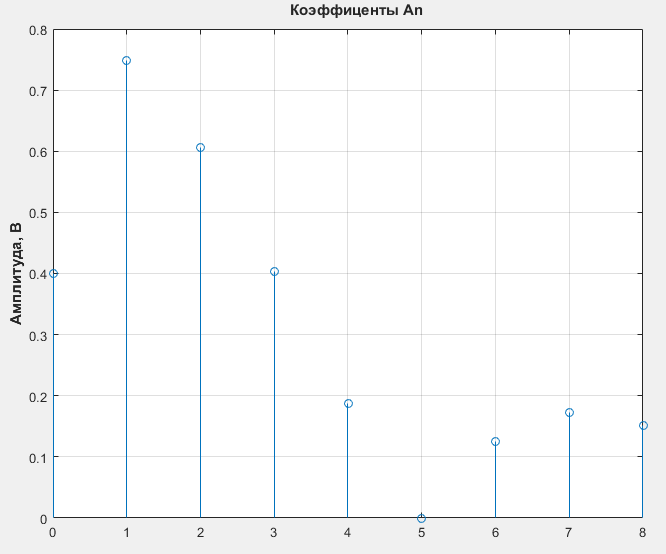
Рис.10 Коэффициенты A_n

Расчет начальных фаз гармоник:

% выводим графики (показан для коэффициентов φ_n)

stem(n, φ_n)

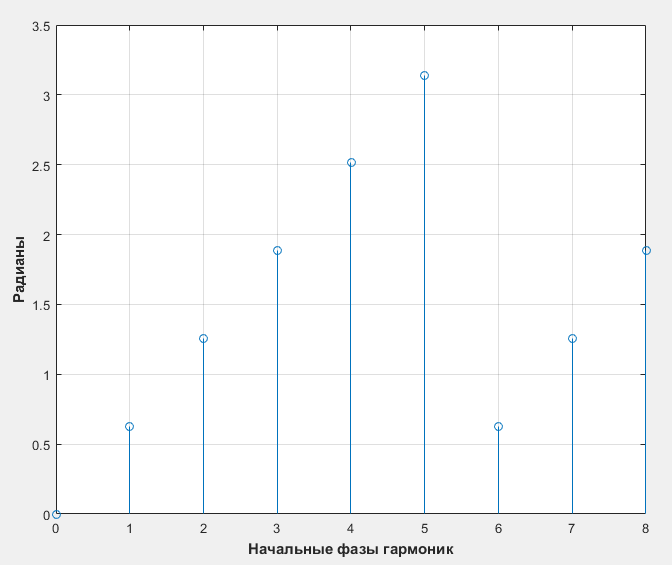
Рис.11 Начальные фазы гармоник φ_n

Далее рассчитываем мощности гармоник.

% выводим графики (показан для коэффициентов Pn)

stem(n, Pn)

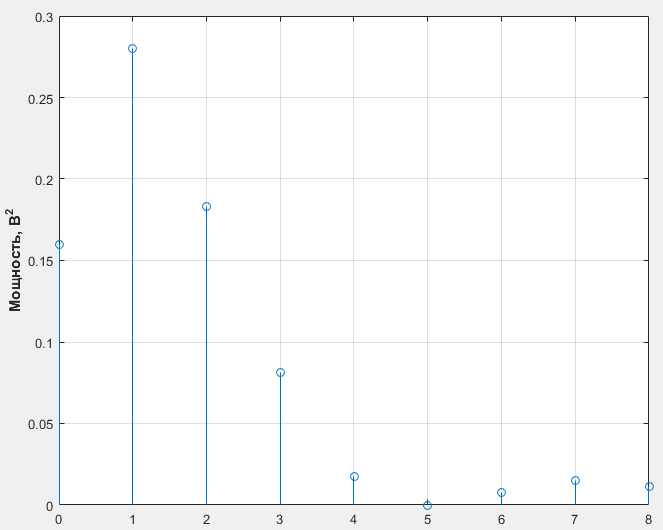
Рис.12 Спектр мощности

Определим суммарную мощность N первых гармоник:

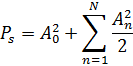
Для N=2: P_s=0.16+0.28+0.1833+0.0815+0.0175=0.7223, В²

Таким образом, если произвести расчет первых четырех гаромник, то получим,что в частотном интервале [0 до 4/Т] сосредоточено примерно 90% средней мощности сигнала. Поэтому можно принять эффективную ширину спектра последовательности прямоугольных импульсов 4/Т=500 Гц. В случае последовательности прямоугольных импульсов ширину спектра, считают с учетом первого нулевого коэффициента. В нашем случае он находится на частоте 675 Гц,таким образом ∆f=675 Гц.

Далее следует восстановить сигнал. Для этого подставим полученные коэффициенты ряда Фурье в сам ряд Фурье, при этом пример N примем равным 9. Воспользуемся программой Maple. Код будет иметь вид:

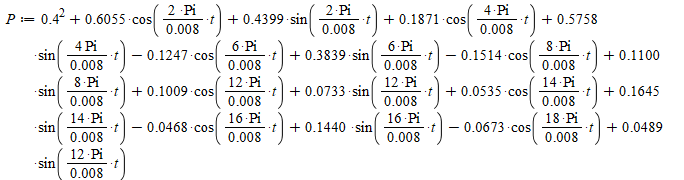
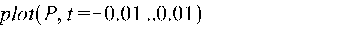
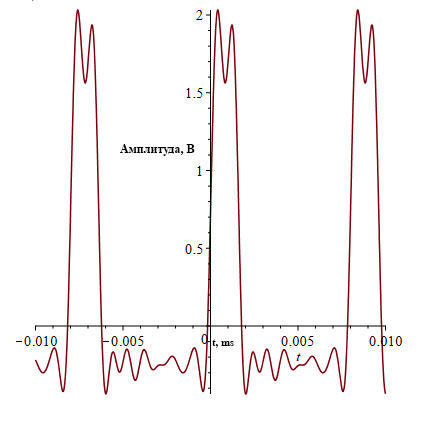
Рис.13 Восстановленный по сумме гармоник сигнала.

При N стремящемся к бесконечности сигнал будет соответствовать исходной послдовательности прямоугольных импульсов.

⇐ Предыдущая 1 2 345 6 7 Следующая ⇒