Решение задания 1.1. Задание 1.2

⇐ ПредыдущаяСтр 2 из 7Следующая ⇒

Решение задания 1.1

Студент –Чернавин Денис Леонидович.

Третья буква фамилии:

«р» - 0х0440 – 0100 0100 0000 – N_ф3=2, U_m₁=2 B, четное.

Вторая буква имени:

«е» - 0x0435 –0100 0011 0101–N_и2=5, U_m₂=5.

Первая буква отчества:

«Л» - 0x041B – 0000 0100 0011 1011–N_o₁=5, k=5.

Количество букв в фамилии студента – 8, Т=8 мс.

Для рассматриваемого варианта, в соответствии, записываем выражение для сигналов и мгновенной мощности:

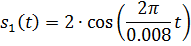
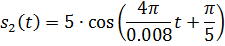
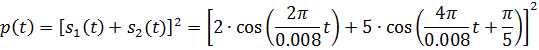
Далее с помощью программы Maple строим графики сигналов, их суммы и мгновенной мощности двух сигналов(рис.1-4). Для этого пишем в программу следующие команды:

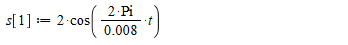
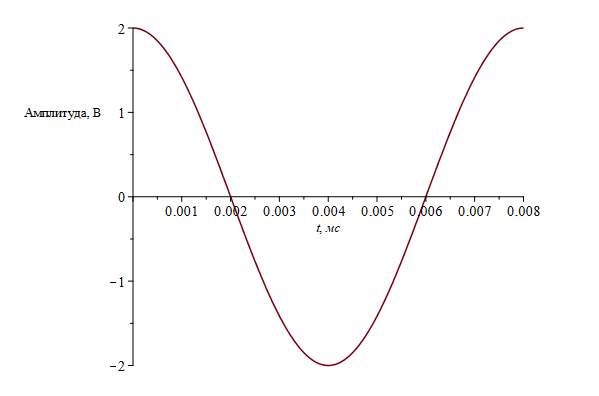
Рис.1 График сигнала s₁(t).

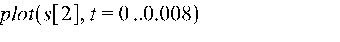
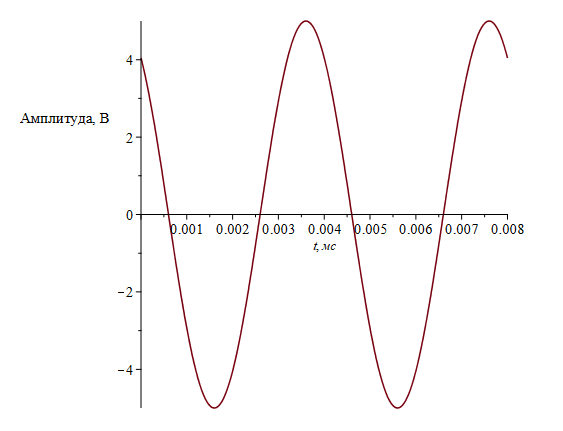
Рис. 2. График сигнала s₂(t).

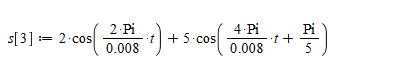
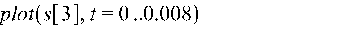
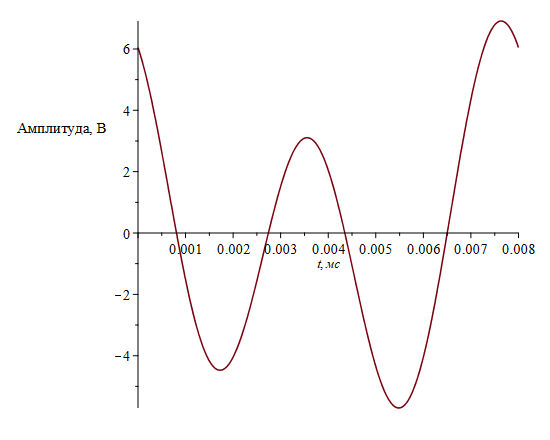
Рис. 3. График суммы сигналов s₁(t) и s₂(t).

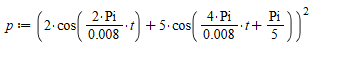
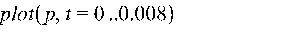
Рис. 4. График функции мощности.

Далее рассчитываем мощности и энергии (взаимной, полной и каждого по отдельности) с помощью программы Matlab. Далее показан код программы:

U1=2;

U2=5;

T=0.008;

N=1024;

dt=T/N;

t=[0:dt:T-dt];

s1=U1*cos(2*pi*t/T);

s2=U2*cos(4*pi*t/T+pi/3);

s=s1+s2;

s3=s1.*s2;

P1=sum(s1.^2)/1024;

P2=sum(s2.^2)/1024;

P=sum(s.^2)/1024;

E1=P1*T;

E2=P2*T;

E=P*T;

E12=round(sum(s3)/1024,4);

Power=sprintf('P1=%g P2=%g P=%g',P1,P2,P)

Energy=sprintf('E1=%g E2=%g E=%g E12=%g', E1,E2,E,E12);

Если мы будем подставлять значения в формулы мощностей и энергии, то получим те же значения, полученные при вычислениях MatLab:

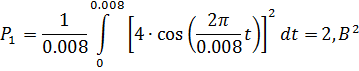
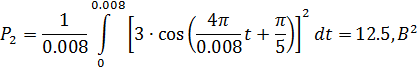
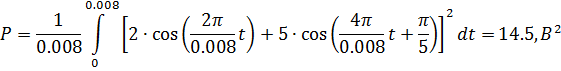
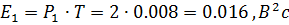
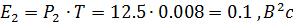
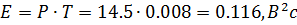
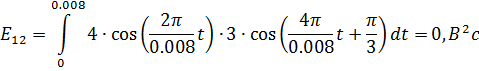
Так как взаимная энергия равна нулю, значит сигналы являются ортогональными.

Задание 1.2

Построить АКФ и ВКФ двух сигналов. Для построения АКФ взять двоичную кодовую комбинацию третьей буквы фамилии в коде UTF. Для построения ВКФ взять двоичные кодовые комбинации третьей буквы фамилии и второй буквы имени в коде UTF. Четыре первых нуля в кодовой комбинации не учитывать.

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒