Задание 4.2. ЗАКЛЮЧЕНИЕ

Задание 4.2

Рассчитать и построить график вероятности ошибки в приёме элементарного символа в зависимости от отношения сигнал/помеха.

Выполнения задания 4.2:

Вторая буква имени студента – «е» - 0х0435 – 0000 0100 0011 0101. Количество «1» - пять, следовательно, 𝑈𝑚 = 5 мВ. Третья буква фамилии «р» имеет кодировку 0х0440 – 0000 0100 0100 0000. Количество «1» - два, следовательно, 𝐻 = 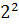= 4. Модуляция – ЧМ, из предыдущего задания.

Введём обозначения:

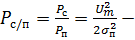отношение сигнал/помеха.

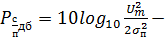отношение сигнал/помеха, дБ.

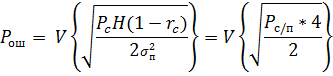
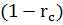=1 при ЧМ

При фиксированном значении 𝑈𝑚 = 5 мВ будем менять 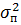и вычислять дополнение к интегралу вероятности. Данные записываем в таблицу 3.

Таблица 3

,
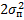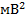
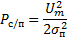
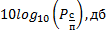
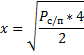
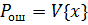
125000	0,0001	- 40	0,0141	0,494
12500	0,001	- 30	0,0447	0,482
1250	0,01	- 20	0,141	0,4438
125	0,1	- 10	0,447	0,3274
50	0,25	-6.0206	0,707	0,2398
25	0,5	-3.0103	1	0,1587
20	0,625	-2.0412	1,118	0,1318
12.5	1	0	1,414	0,0786
6.25	2	3.0103	2	0,0228
5	2,5	3.9794	2,236	0,0127

Программа расчёта с помощью MatLab.

sigma=[125000 12500 1250 125 50 25 20 12.5 6.25 5]; %строка мощностей помехи +

Psp=12.5./sigma; % отношение сигнал/помеха

PspdB=10*log10(Psp); % отношение сигнал/помеха, дБ

x=sqrt(Psp.*2); % расчёт значений х

error=0.5*erfc(x/sqrt(2)); % расчёт дополнения к интегралу вероятности

semilogy(PspdB, error, 'k', 'LineWidth', 2) % вывод графика

title('Зависимость вероятности ошибки от отношения сигнал/помеха')

xlabel('Отношение сигнал/помеха, дБ')

ylabel('Вероятность ошибки, Рош')

grid on

Psp =0.0001 0.0010 0.0100 0.1000 0.2500 0.5000 0.6250 1.0000 2.0000 2.5000 P

spdB =-40.0000 -30.0000 -20.0000 -10.0000 -6.0206 -3.0103 -2.0412 0 3.0103 3.9794

x =0,0141 0,0447 0,141 0,447 0,707 1 1,414 2 2,236

error =0,494 0,482 0,4438 0,3274 0,2398 0,1587 0,1318 0,0786 0,0228 0,0127

По результатам расчёта строим график в логарифмическом масштабе.

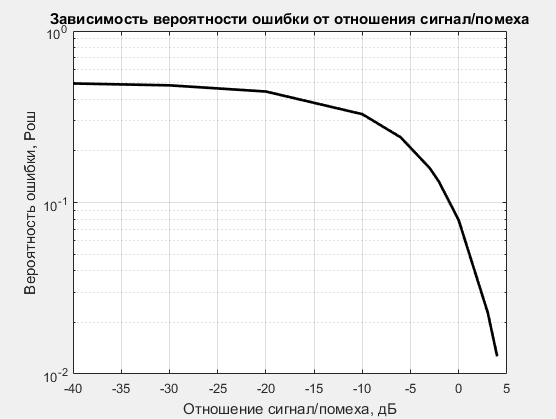
Рис. 3. Результаты расчёта

ЗАКЛЮЧЕНИЕ

В ходе курсовой работы был рассчитан источник сообщений, произведены статистическое кодирование буквенного сообщения методом Шеннона-Фано, помехоустойчивое кодирование циклическим кодом, определены синдромы для всех вариантов одиночных ошибок. Составлена временная диаграмма модуляции двоичного сообщения. Рассчитан и построен график вероятности ошибки в приёме элементарного символа в зависимости от отношения сигнал/помеха.

Список литературы:

1. Гоноровский, И.С. Радиотехнические цепи и сигналы. – 5-е изд. – М.:Дрофа,2006. – 719с. – ISBN 5-7107-7985-7.

2. Стафеев, А.В. Разуваев, В.А. Теория связи: метод. указания к курсовой работе/ А.В.Стафеев, В.А. Разуваев. – Хабаровск: Изд-во ДВГУПС. 2018. – 34 с.: ил.

3. Баскаков, С. И. Радиотехнические цепи и сигналы. — 3-е изд. — М.: «Высшая школа», 2005. — 464 с. — ISBN 5-06-003843-2.

4. Кудряшов, Б.Д. Теория информации. - СПб.: Питер, 2009. - 320 с. - ISBN: 978-5-388-00178-8.

5. Зюко, А. Г., Фалько, А. И. Помехоустойчивость и эффективность систем передачи информации. — М.: Радио и связь, 1985. – 271 с.

6. http://www.scilab.org/

7.Ю. А. Брюханов, А. Л. Приоров Общая теория связи. Учебное пособие, Ярославль ЯрГУ, 2014

8. Гельгор А.Л. Общая теория связи. Проверка статистических гипотез. Оценивание параметров. Оптимальный приём сигналов: учеб. пособие / Гельгор А.Л., Горлов А.И., Попов Е.А. — СПб.: Изд-во Политехн. ун-та, 2013. — 227 с.

9. Павликов С. Н., Убанкин Е. И., Левашов Ю.А.. Общая теория связи. [Текст]: учеб. пособие для вузов – Владивосток: ВГУЭС,2016. – 288 с.. 2016

10. Аджемов А.С., Санников В.Г. Общая теория связи. - ISBN 978-5-9912-0690-7

⇐ Предыдущая 1 2 3 45