
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЯ
3.ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЯ
Задание 3.1
Произвести помехоустойчивое кодирование циклическим кодом двоичного сообщения, состоящего из третьей буквы фамилии студента (без четырёх нулей в начале). Определить синдромы для всех вариантов одиночных ошибок.
Выполнения задания 3.1:
Фамилия - Чернавин. Третья буква фамилии – «р».
Записываем в двоичном виде, «р» - 0х0440 – 0000 0100 0100 0000. Без четырёх первых нулей: 0100 01000 0000.
Математическая запись:
𝐾(𝑥) = 0 ∙ 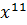 + 1 ∙
+ 1 ∙ 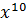 + 0 ∙
+ 0 ∙ 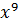 + 0 ∙
+ 0 ∙ 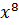 + 0 ∙
+ 0 ∙ 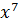 + 1 ∙
+ 1 ∙ 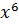 + 0 ∙
+ 0 ∙ 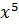 + 0 ∙
+ 0 ∙ 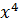 +
+
+ 0 ∙ 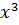 3 + 0 ∙
3 + 0 ∙ 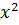 + 0 ∙
+ 0 ∙ 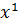 + 0 ∙
+ 0 ∙ 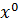
𝐾(𝑥) = 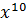 +
+ 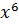 .
.
k=11 - колличество информационных символов
Рассчитываем колличество проверочных символов - r:
𝑟 =⌈ 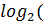 k + 1)⌉ = ⌈
k + 1)⌉ = ⌈ 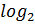 (11 + 1)⌉ = ⌈3,585⌉ = 4
(11 + 1)⌉ = ⌈3,585⌉ = 4
Выбираем порождающий полином четвёртой степени:
G(x)= 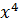 +x+1.
+x+1.
Умножаем K(x) на 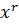 :
:
𝐾(𝑥) ∙ 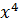 =
= 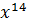 +
+ 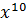
Для нахождения остатка R(x) производим деление:
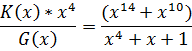
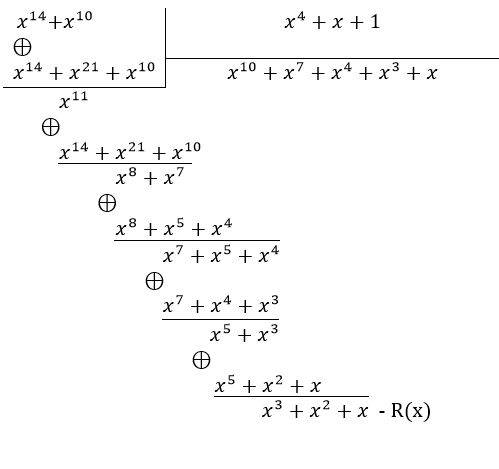
Кодовая комбинация будет иметь вид:
𝑁(𝑥) = 𝐾(𝑥) ∙ 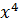 + 𝑅(𝑥) =
+ 𝑅(𝑥) = 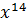 +
+ 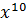 +
+ 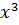 +
+ 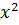 + x
+ x
В двоичном виде: 100 0100 0000 1110. Четыре последних разряда являются проверочными.
Таблица 2
| Разряд с ошибкой | Вектор ошибки | Принятая кодовая комбинация N”(x) | Остаток от деления N”(x)/G(x) (синдром ошибки | Синдром ошибки в двоичном виде |
| Ошибки нет | 000 0000 0000 0000 | 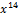 + + 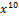 + +  + +  + x + x
| ||
| 000 0000 0000 0001 | 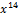 + + 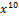 + +  + +  + + 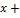 1 1
| |||
| 000 0000 0000 0010 | 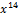 + + 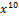 + +  + + 
| x | ||
| 000 0000 0000 0100 | 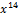 + + 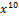 + +  + x + x
| 
| ||
| 000 0000 0000 1000 | 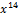 + + 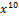 + +  + +  + x + x
| 
| ||
| 000 0000 0001 0000 | 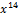 + + 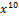 + + 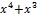 + +  + x + x
| x+1 | ||
| 000 0000 0010 0000 | 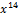 + + 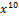 + + 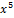 + +  + +  + x + x
|  +x +x
| ||
| 000 0000 0100 0000 | 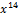 + + 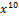 + + 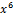 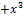 + +  + x + x
|  + + 
| ||
| 000 0000 1000 0000 | 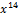 + + 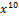 + + 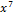 + +  + +  + x + x
|  +x+1 +x+1
| ||
| 000 0001 0000 0000 | 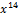 + + 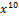 + + 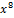  + +  + x + x
|  +1 +1
| ||
| 000 0010 0000 0000 | 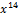 + + 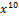 + + 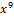 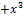 + +  + x + x
|  +x +x
| ||
| 000 0100 0000 0000 | 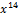 + +  + +  + x + x
|  +x+1 +x+1
| ||
| 000 1000 0000 0000 | 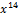 + + 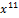 + + 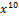 + +  + +  + x + x
|  + +  +x+ +x+
| ||
| 001 0000 0000 0000 | 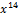 + + 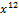 + + 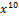 + +  + +  + x + x
|  + +  +x+1 +x+1
| ||
| 010 0000 0000 0000 | 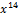 + + 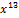 + + 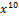 + +  + +  + x + x
|  + +  +1 +1
| ||
| 100 0000 0000 0000 | 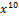 + +  + +  + x + x
|  +1 +1
|
Таким образом, каждому вектору ошибки соответствует свой синдром. Поэтому, зная синдром, можно определить в каком разряде принятой кодовой комбинации произошла ошибка и исправить её.
Циклический код в программе MatLab
В соответствии с этим перепишем заданную кодовую комбинацию K для буквы «а» 00000010001, и соответствующий ей полином:
𝐾(𝑥) = 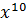 +
+ 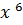
В нашем случае n=15, k=11.
Находим все возможные генераторные (порождающие) полиномы:
>> n=15;
>> k=11;
>> G = cyclpoly(n,k,'all');
>> G =
1 0 0 1 1
1 1 0 0 1
1 1 1 1 1
Для соответствия с ранее рассчитанным примеров, выбираем полином из второй строки G(𝑥) = 1 + 𝑥+ 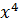 и вводим в двоичном виде в программу:
и вводим в двоичном виде в программу:
>> G =[1 1 0 0 1];
Рассчитаем проверочную матрицу (синдромы ошибки):
>> parmat = cyclgen(n,G);
>> parmat
1 0 0 0 1 0 0 1 1 0 1 0 1 1 1
0 1 0 0 1 1 0 1 0 1 1 1 1 0 0
0 0 1 0 0 1 1 0 1 0 1 1 1 1 0
0 0 0 1 0 0 1 1 0 1 0 1 1 1 1
Столбцы полученной матрицы соответствуют ранее полученным синдромам ошибки. Нулевой синдром здесь не учитывается.
Вводим в программу кодовую комбинацию, подлежащую кодированию:
>> K=[0 0 0 0 0 0 1 0 0 0 1];
Производим кодирование:
>> N = encode(K, n, k, 'cyclic/binary', G);
>> N
0 1 1 1 0 0 0 0 0 0 1 0 0 0 1
Запишем в виде полинома:
N(x)= 𝑥+ 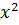 +
+ 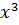 +
+ 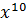 +
+ 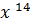
Произведём декодирование при отсутствии ошибки:
>> decN = decode(N, n, k, 'cyclic/binary', G);
>> decN
0 0 0 0 0 0 1 0 0 0 1
Результат совпадает с исходной кодовой комбинацией. Введём ошибку, например, в седьмой разряд:
>> N(7) = ~N(7);
>> N
0 1 1 1 0 0 1 0 0 0 1 0 0 0 1
Произведём декодирование с ошибкой в принятой кодовой комбинации:
>> decN = decode(N, n, k, 'cyclic/binary', G);
>> decN
0 0 0 0 0 0 1 0 0 0 1
Результат также совпадает с исходной кодовой комбинацией. Однократная ошибка исправлена
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|