Асимптоты. План исследования графика функции

5. Асимптоты

Определение 7.Прямая 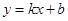называется асимптотой для кривой 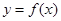, если расстояние от точки М, лежащей на кривой, до прямой стремится к нулю при удалении точки М от начала координат в бесконечность.

Существует три вида асимптот: вертикальные, горизонтальные и наклонные.

Определение 8. Прямая 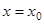называется вертикальной асимптотой графика функции 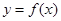, если выполнено хотя бы одно из условий:

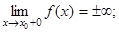
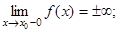
т.е. точка 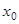является точкой разрыва второго рода.

Определение 9. Прямая 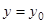называется горизонтальной асимптотой графика функции 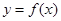, если .

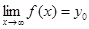Определение 10. Прямая 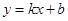называется наклонной асимптотой графика функции 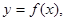если существуют числа k и b такие, что

, .

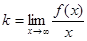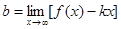Замечание. Если оба предела существуют и конечны (т.е. равны числам), причем 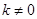, то существует и наклонная асимптота. Если k = 0, то получим горизонтальную асимптоту. Ес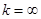ли или 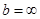, то наклонных асимптот не существует.

6. План исследования графика функции

1. Найти область определения функции.

2. Найти область непрерывности функции и точки разрыва. Определить характер точек разрыва.

3. Найти нули функции (точки пересечения с координатными осями).

4. Установить, не является ли график функции симметричным относительно какой-нибудь прямой (или координатной оси) или точки, т.е. проверить, является функция четной, или нечетной, или ни той и ни другой.

5. Проверить функцию на периодичность.

6. Найти промежутки монотонности и экстремумы.

7. Найти промежутки выпуклости и точки перегиба.

8. Найти асимптоты.

9. Найти несколько дополнительных значений функции.

10. Построить график.

⇐ Предыдущая 1 2 34