Выпуклость и вогнутость.. Теорема 4.

4. Выпуклость и вогнутость.

Пусть функция 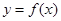дифференцируема в любой точке интервала (a, b). Тогда существует касательная к графику функции в любой точке графика.

Определение 4. Непрерывная функция 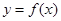называется выпуклой вниз (т.е. вогнутой) (рис.3), если все точки кривой лежат выше любой ее касательной к графику 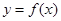на интервале (a, b). И называется выпуклой вверх (рис.4), если все точки кривой лежат ниже этих касательных.

Рис.3 Рис.4

Теорема 4.

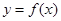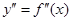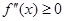Если функция имеет на интервале (a, b) конечную вторую производную и во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вниз (вогнут). Если 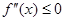во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вверх.

Определение 5.Точки, при переходе через которые функция меняет направление выпуклости, называются точками перегиба функции .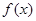

Определение 6.Точка 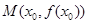называется точкой перегиба графика функции 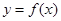, если существует такая окрестность точки 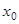, в пределах которой график функции слева и справа от точки х₀ имеет разные направления выпуклости.

Теорема 5. (необходимое условие существования точки перегиба).

Если функция 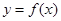дважды дифференцируема в точке 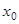, непрерывна в этой точке, и ее график имеет перегиб в точке 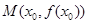, тогда .

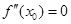Теорема 6. (достаточное условие существования точки перегиба).

Пусть функция 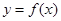имеет вторую производную 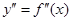в некоторой окрестности точки 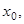и пусть 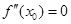, либо 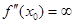, либо 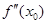не существует, тогда, если в пределах указанной окрестности вторая производная 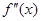имеет разные знаки слева и справа от точки х₀, то график функции имеет перегиб в точке .

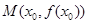Замечание.Точка разрыва не является точкой перегиба, хотя при переходе через нее кривая зачастую меняет направление выпуклости.

⇐ Предыдущая 1 234 Следующая ⇒