Экстремумы.. Наибольшее и наименьшее значение функции на отрезке.

2. Экстремумы.

пределение 2.Точка, отделяющая промежуток возрастания от промежутка убывания и наоборот, называется точкой экстремума.

Определение 3. Пусть функция 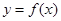определена на [a, b]. Точка 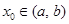называется точкой максимума функции 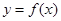, если для любого х из некоторой достаточно малой окрестности точки 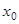выполняется неравенство 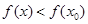. Точка 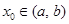называется точкой минимума функции 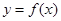, если для любого х из некоторой достаточно малой окрестности точки 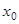выполняется неравенство .

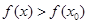Точки максимума и минимума называютсяточками экстремума.

Теорема 2. (Необходимое условие существования экстремума).

Если функция 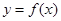дифференцируема в точке 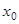и имеет в этой точке экстремум, то

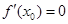Точки, в которых производная равна нулю, называются стационарными, а точки, в которых производная равна нулю или терпит разрыв, называются критическими. Все точки экстремума функции находятся среди ее критических точек.

Теорема 3. (Достаточное условие существования экстремума).

Если при переходе через критическую точку 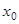производная меняет знак

1) с «+» на «–», то 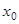– точка максимума,

2) с «–» на «+», то 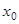– точка минимума,

3) если не меняет знак, то в критической точке экстремума нет.

3. Наибольшее и наименьшее значение функции на отрезке.

1) находят на 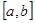экстремумы;

2) определяют значения 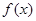на концах ;

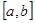3) из всех полученных значений выбирают наибольшее и наименьшее.

Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и другие задачи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольших и наименьших значений. Решением таких задач занимается особый раздел математики – линейное программирование.

⇐ Предыдущая 123 4 Следующая ⇒