Исследование функций с помощью производных

Исследование функций с помощью производных

1. Возрастание и убывание функций

Теорема 1.

Если во всех точках х некоторого промежутка D производная функции 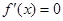, то функция 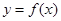постоянна на этом промежутке.

Доказательство

Функция 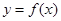удовлетворяет всем условиям теоремы Лагранжа, т.е. для любых точек 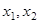из промежутка D существует точка 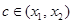такая, что справедлива формула конечных приращений Лагранжа: 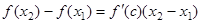. По условию теоремы 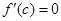, следовательно, 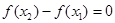. Отсюда 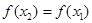. Это означает, что функция 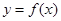постоянна на этом промежутке, что и требовалось доказать.

Теорема 2.

Для того чтобы дифференцируемая на интервале (a, b) функция 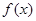была возрастающей, необходимо и достаточно, чтобы выполнялось условие

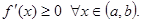(1)

Аналогично условие

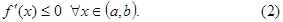
является необходимым и достаточным для убывания функции 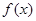на интервале (a, b).

Доказательство

Необходимость

Пусть 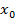– произвольная точка интервала (a, b). Из определения возрастающей функции имеем:

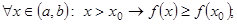
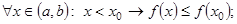
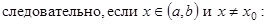
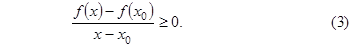
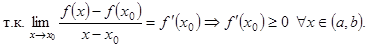
Достаточность

Пусть выполняется условие (1) и 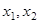- произвольные точки из промежутка (a, b), причем 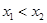. Тогда по теореме Лагранжа существует точка 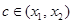такая, что справедлива формула конечных приращений Лагранжа:

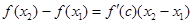По условию теоремы 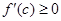и 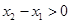, следовательно, 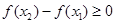. Отсюда, 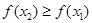, т.е. функция не убывает, что и требовалось доказать.

Определение 1. Промежутки возрастания и убывания называются промежутками монотонности.

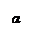
Рис.1 Рис.2

Геометрический смысл: если 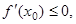то угол α – тупой (рис.1), если то угол α – острый (рис.2).

12 3 4 Следующая ⇒