Нормальное распределение Гаусса

№19.Нормальное распределение Гаусса

В большинстве практических случаев при чисто случайных разбросах результатов отдельных измерений относительно истинного значения измеряемой величины функция распределения имеет вид, получивший название нормального распределения Гаусса.

Если причины, вызывающие отклонения результатов измерения от истинного значения, настолько разнообразны и многоплановы, что невозможно выделить какую-либо доминанту, функция распределения всегда имеет вид экспоненты с определенными параметрами. К этому утверждению следует относиться как к аксиоме физики, т. е. мир устроен так, что при случайном выпадении многократных результатов повторяющихся событий функция распределения будет иметь вид экспоненты. В метрологии, как и в физике вообще, встречается достаточно много аксиом, например постоянство скорости света, корпускулярно-волновой дуализм, токи смещения в уравнениях Максвелла, принцип относительности и т. д. Аналитическую зависимость функции нормального распределения можно отнести к категории таких принципов или аксиом. В метрологии и в технике измерений получение такой зависимости неоценимо в определении достоверности, правильности и точности измерений. Предложенная Гауссом зависимость дифференциальной функции распределения результатов повторяющихся случайных событий оказалась настолько ценной, что в Германии, например, формула нормального распределения считается одним из самых крупных достижений науки.

Нормальное распределение выпадения определенного результата в повторяющихся случайных событиях это такое распределение, дифференциальная функция распределения которого имеет вид:

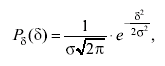(3.42)

где δ = х - m_F; здесь: х - результат однократного измерения; m_F - математическое ожидание результата измерения так, что

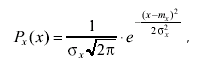(3.43)

где σ_x - среднее квадратическое отклонение результатов измерения.

При записи в таком виде кривые нормального распределения зависят от среднего квадратического отклонения. При увеличении σ распределение все более расплывается, т. е. вероятность появления больших отклонений от математического ожидания увеличивается, а вероятность меньших погрешностей сокращается (рис. 3.6 ).

Для того чтобы сделать аналитическую зависимость нормального дифференциального распределения более универсальной, делают замену переменных, выражая отклонения величины х от математического ожидания m_F в единицах среднего квадратического отклонения:

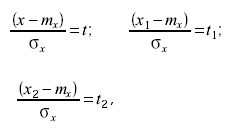(3.44)

где х - результат отдельного измерения; x₁ - минимальное возможное значение измерения; x₂ - максимальное возможное значение измерения. После такой замены переменных вероятность попадания результата измерения в некоторый заданный интервал (x₁ ; x₂ ] выражается как:

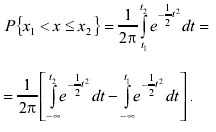(3.45)

Интегралы в скобках не выражаются в элементарных функциях. Их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией

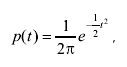(3.46)

график которой изображен на рис. 3.7 .

Функция p(t) не зависит от параметров распределения, в силу чего может быть затабулирована. Значения этой функции в пределах изменения t от нуля до 4 приведены в приложении II.

Интегральная функция нормального распределения имеет вид:

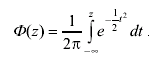(3.47)

По физическому смыслу это есть вероятность того, что погрешность измерения будет меньше или равна величине z, т. е.

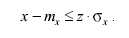(3.48)

Интегральная функция нормального распределения также затабулирована (см. приложение I).

Используя интегральную функцию нормального распределения, можно определить вероятность попадания результата измерения в интервал (x₁ , x₂ ] как

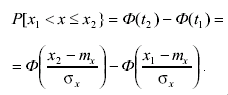(3.49)

При этом справедливо тождество:

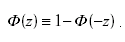(3.50)

Подчеркнем, что все сказанное справедливо, если погрешности случайные, распределение можно считать нормальным с известной дисперсией σ_x² . Тогда на основании формулы (3.44) имеем:

(3.51)

Обычно значения t₁ и t₂, выбирают симметрично по обе стороны от максимума распределения так, что t₁ = t₂ = t_p. Формула для вероятности попадания результата в заданный интервал приобретает вид:

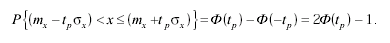(3.52)

Меняя х и m_F местами в этом неравенстве, получим:

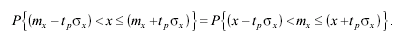(3.53)

Если систематические погрешности исключены и m_F = Q, то

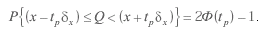(3.54)

Это означает, что истинное значение измеряемой величины с доверительной вероятностью Р = 2Ф(t_p) -1 находится между границами интервала [(х -t_pσ_x );(х+t_pσ_x )] . Интервал от -t_pσ_x до +t_pσ_x называется доверительным интервалом погрешности измерения, а половина интервала t_pσ_x называется доверительной границей случайного отклонения результатов наблюдения, соответствующей доверительной вероятности Р.

Для определения доверительной границы задаются доверительной вероятностью Р и по формуле 3.51 находят из таблиц параметр t_p. После этого вычисляют доверительное отклонение t_pσ_x . Если известно среднее квадратическое отклонение результатов измерения, то легко определить погрешность измерения при заданной доверительной вероятности.

Задача может быть поставлена иначе, а именно: какова доверительная вероятность попадания результата измерения в заданный доверительный интервал, если известно среднее квадратическое отклонение серии измерений? В этом случае определяют параметр t_p делением доверительного интервала на среднеквадратическое отклонение t_p= (t_pσ_x ) /σ_x . Затем из таблиц значений интегральной функции нормального распределения находят величину Ф(t_p), после чего вычисляют доверительную вероятность как 2Ф(t_p) -1.

Из приведенных определений понятий, определяющих нормальное распределение вероятности получения определенных результатов измерения можно кратко сформулировать следующие выводы:

1. Погрешности измерения (интервалы допустимой погрешности) зависят от того, с какой вероятностью мы хотим получить достоверный результат.

2. Для определения погрешности при заданном доверительном интервале и для определения этого интервала при заданной доверительной вероятности необходимо знать среднее квадратическое отклонение результатов измерения.

3. Функции нормального распределения дают связь между вероятностью попадания результатов измерения (доверительной вероятностью) в заданный интервал и величиной самого интервала, называемого доверительной границей случайного отклонения.

№20.Нормальное распределение при ограниченном числе наблюдений. Распределение Стьюдента

Сформулированные в предыдущем разделе понятия и написанные формулы относятся к случаю, когда число измерений бесконечно велико. На практике мы всегда имеем дело с ограниченным числом измерений, и задача, которая всегда стоит перед оператором, состоит в том, как оценить точность измерений, т. е. найти его меру приближения к истинному значению на основании группы результатов наблюдения. Эта задача есть частный случай статистической задачи нахождения параметров функции распределения, в первую очередь среднего квадратического отклонения, на основе выборки, т. е. ряда значений, принимаемых этой величиной в результате п независимых опытов.

В результате отдельных измерений мы получаем некоторые строго фиксированные результаты (точки) измеряемой величины. Их значения являются случайными с некоторым распределением, зависящим как от самой величины, так и от числа опытов. При случайном разбросе значений рассеяние (или среднее квадратическое отклонение) в большинстве случаев определяется характером и величиной случайных хаотических воздействий или на средство измерения, или на объект измерения, или на оператора.

К точечным оценкам теория случайных погрешностей предъявляет совершенно определенные требования, которые можно сформулировать следующим образом:

1. Оценка должна быть состоятельной, т. е. при увеличении числа опытов она должна приближаться к истинному значению измеряемой величины - должна сходиться по вероятности.

2. Оценка должна быть несмещенной, то есть ее математическое ожидание должно быть равно измеряемой величине.

3. Оценка должна быть эффективной, то есть ее дисперсия должна быть меньше дисперсии любой другой оценки данного параметра.

Пусть есть ряд результатов отдельных измерений x₁ ; x₂ ; x₃ ;...... x_n , где

n - число наблюдений. Математическое ожидание и дисперсия записываются как

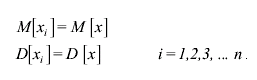(3.55)

За оценку истинного значения измеряемой величины естественно принять значение среднего арифметического, т. е.:

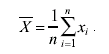(3.56)

Эта оценка математического ожидания результата измерений может стать оценкой истинного значения измеряемой величины после исключения систематической погрешности.

Поскольку среднее арифметическое вычислено на основании ограниченного ряда измерений, оно само является величиной случайной. Вычислим его математическое ожидание:

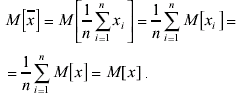(3.57)

Это значит, что среднее арифметическое является несмещенной оценкой истинного значения. Однако несмещенными будут и все другие оценки вида:

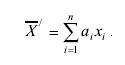(3.58)

если 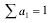. Покажем, что из всех определенных так оценок, наименьшую дисперсию имеет среднее арифметическое

В теории погрешности показывается, что последняя сумма 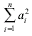достигает минимума, если все а одинаковы и равны 1/n. Тогда дисперсия среднего арифметического равна:

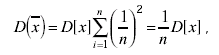(3.59)

т. е. дисперсия среднего арифметического в n раз меньше дисперсии результата отдельного наблюдения. В терминах среднего квадратического отклонения это имеет вид:

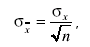(3.60)

т. е. среднее квадратическое отклонение среднего арифметического в 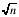раз меньше среднего квадратического отклонения результата отдельного наблюдения. По мере увеличения числа наблюдений

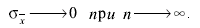(3.61)

Логическим следствием сказанного является оценка истинного значения измеряемой величины по результатам отклонения от среднего арифметического:

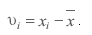(3.62)

В качестве точечной оценки дисперсии случайной погрешности естественно выбрать величину

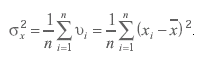(3.63)

Эта оценка состоятельна и эффективна, но немного смещена, поскольку ее математическое ожидание составляет

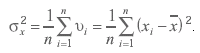(3.64)

Точечную оценку среднего квадратического отклонения результата отдельного измерения принято определять как

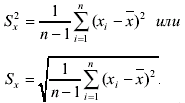(3.65)

Эта оценка есть тоже случайная величина, т. е. при повторении серии из п измерений мы получим несколько иное S\ значение оценки среднего квадратического отклонения. Поскольку среднее арифметическое значение имеет дисперсию в 1/n раз меньшую, чем результат для отдельного измерения, точечная оценка дисперсии (среднего квадратического отклонения) для среднего арифметического имеет вид:

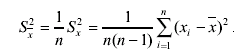(3.66)

где S_x² - среднее квадратическое отклонение для результата отдельного измерения.

Общий итог введения понятий для нормального распределения вероятности для ограниченного числа измерений можно записать в виде

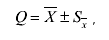(3.67)

где Q - истинное значение измеряемой величины, равное математическому ожиданию Q=m_F; 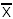- среднее арифметическое значение результатов серии независимых измерений; - среднее квадратическое отклонение среднего арифметического при повторении серии измерений.

При увеличении числа измерений доверительный интервал сокращается в 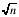раз. Этот очень важный вывод теории погрешностей позволяет с любой наперед заданной вероятностью в принципе сколь угодно близко подойти к истинному значению измеряемой величины, увеличивая число независимых измерений.

Как итог, при нормальном распределении случайных погрешностей мы имеем тесную взаимосвязь между желаемым отклонением от истинного значения измеряемой величины, доверительной вероятностью данного отклонения и числом независимых измерений. Соответственно, задача может быть поставлена в нескольких вариантах:

1. Определить доверительный интервал, если необходимо получить заданную доверительную вероятность при фиксированном числе измерений.

2. Определить доверительную вероятность попадания среднего арифметического значения определенного числа независимых измерений в заданный доверительный интервал.

3. Определить необходимое число независимых измерений, если считать известной доверительную вероятность и задаться определенным доверительным интервалом.

При ограниченном числе измерений доверительный интервал, введенный нами для распределения Гаусса, записывается в виде

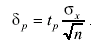(3.68)

Результат измерений приобретает вид:

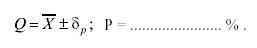(3.69)

Если при измерениях имеется возможность проведения ограниченного числа измерений, но дисперсия результатов неизвестна, то функция распределения должна зависеть не только от желаемой доверительной вероятности и доверительного интервала, но и от числа независимых измерений. В этом случае вместо распределения Гаусса используется несколько иное распределение, называемое распределением Стьюдента, которое имеет следующую аналитическую зависимость:

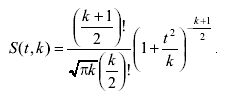(3.70)

где k - число степеней свободы распределения, равное числу независимых измерений без единицы k = (n -1), а параметр t называется дробью Стьюдента и определяется как

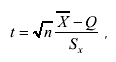(3.71)

где сохранены предыдущие обозначения, т. е. n - число независимых измерений; - среднее арифметическое значение серии измерений; Q -истинное значение измеряемой величины и S_x - оценка среднего квадратического отклонения результата измерения (формула 3.65).

Вероятность того, что в результате измерения дробь Стьюдента примет некоторое значение в интервале(-t; +t)равна

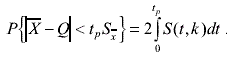(3.72)

Значения функции S(t, k) были вычислены и затабулированы Фишером для различных значений доверительной вероятности Р в пределах от 0,10до 0,99 при k =1, 2,...... 30. Эти значения приведены в приложении.

С помощью распределения Стьюдента может быть найдена вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает

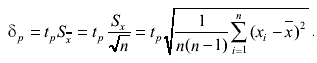(3.73)

Итог записывается в прежнем виде: Q = Х + 8 ; при Р =.....%. Таблицы значений интегралов функции S(t,k) распределения Стьюдента , приведенные в приложении III, определяют доверительную вероятность Р как функцию двух параметров - t и k. По этой таблице, следовательно, можно, зная два из этих трех значений, найти третье, т. е. по числу измерений и доверительному интервалу либо найти доверительную вероятность, либо по числу измерений и доверительной вероятности найти доверительный интервал, либо по доверительной вероятности и доверительному интервалу найти необходимое число независимых измерений, которые необходимо выполнить. Например, зная число опытов п, найдем число степеней свободы к = п - 1. Задавшись доверительной вероятностью Р, определим соответствующее ей значение дроби Стьюдента t по таблице. Затем по формуле 3.73 находим доверительный интервал.

Проиллюстрируем возможности оценки случайной погрешности с использованием распределения Стьюдента на примере.

Пример:

Даны некоторые результаты измерения длины при числе независимых измерений, равных 5. Получен следующий результат:

L= (15,785+0,005) мм
(среднее квадратическое отклонение = 0,005 мм).

Вопрос: Какова вероятность того, что при этом длина будет измерена с точностью δ_i = 0,01 мм?

Решение: 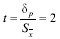; k= 5 -1 =4. Из таблицы находим для t=2 и к =4

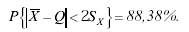
В той же задаче найти доверительную границу погрешности результата измерений при доверительной вероятности 99%.

По таблице для Р = 99 и к = 4 находим t = 4, 604. Следовательно

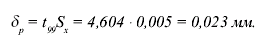
В заключение раздела, посвященного расчету случайных погрешностей, приведем некоторую шутливую аналогию. Поставим вопрос так: каков процент попадания мяча в ворота при реализации футбольных пенальти и от чего это за висит? Пусть при этом не будет учитываться роль вратаря.

Любой представляющий себе футбольную ситуацию ответит, что все достаточно очевидно. Во-первых, многое зависит от мастерства того, кто пробивает пенальти. Это аналог класса точности прибора. Очевидно, что мастер футбола добьется лучшего результата, т. е. либо процент попадания в серии у него будет выше, либо определенное число голов он забьет с меньшего числа попыток. Во-вторых, процент забитых голов зависит от размера ворот. Это аналог доверительного интервала. В очень широкие ворота и новичок забьет большой процент голов. И, наконец, число забитых голов зависит от количества ударов. Даже очень плохой футболист может забить сколько угодно голов, если ему дать достаточно большое число попыток. Разница между мастером и новичком будет лишь в том, что мастер сделает это с меньшего числа попыток. Важно при этом учитывать, что разница в классе игроков особенно скажется при наборе статистики, т. е. при большом числе попыток. Если назначить один или два удара, то и классный игрок может случайно промахнуться, равно как и новичок может с одного-двух раз добиться хорошего успеха. Однако, при большом количестве попыток статистика возьмет свое: классный игрок забьет настолько больше голов, насколько выше его класс.

Этой аналогией мы завершим изложение основных выводов теории погрешностей и отметим основной момент, отличающий профессиональную метрологическую оценку погрешностей от тех оценок, которыми пользовался каждый в оформлении школьных лабораторных работ. Основное отличие в вероятностном характере оценок, т. е. называя те или иные отклонения результатов измерения от истинного значения или от среднего арифметического, нужно всегда указывать, с какой вероятностью мы попадем в заданный интервал отклонений. И еще один, очень важный момент: разброс значений измеряемых величин убывает как корень квадратный из числа повторяющихся независимых измерений. Это значит, что случайную погрешность можно свести к минимуму, увеличивая число измерений.

Последний вывод оказывается очень важным и удивительным: не зная природу погрешности при чисто случайном ее разбросе можно сделать измерения достаточно точными, даже располагая не очень точным средством измерения. В этом минимизация случайных погрешностей значительно проще учета систематической погрешности, для оценки которой иногда нужны широкомасштабные исследования.

⇐ Предыдущая 1 2 3 45