Равномерное распределение случайных погрешностей

№17.Равномерное распределение случайных погрешностей

Часто при измерениях заранее известно, что возможные значения случайных погрешностей средства измерения равновероятны и лежат в пределах некоторого определенного интервала. Такое распределение называется равномерным. Значения дифференциальной функции такого распределения в определенном интервале {-α; +α] постоянны, а вне этого интервала равны нулю. Дифференциальная функция распределения случайной погрешности в этом случае имеет вид:

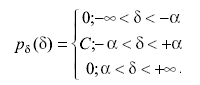(3.35)

Постоянную величину С в равномерном распределении находят из условия, что площадь между кривой распределения и осью абсцисс должна равняться единице, т. е.:

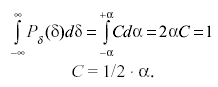(3.36)

Уравнение для интегральной функции равномерного распределения находится из условия, что F_δ(δ) = 0 до тех пор, пока δ< -α. В пределах интервала [-α, +α]:

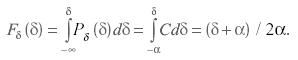(3.37)

Это означает, что интегральная функция равномерного распределения растет от значения F_δ(δ)=0 при δ= -α до F_δ(δ)=1 при δ=+α. При прохождении абсциссы через нуль интегральная функция равна 0,5. Окончательное выражение для интегральной функции распределения имеет вид:

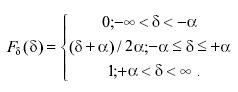(3.38)

Математическое ожидание случайной погрешности при равномерном распределении легко найти из его определения:

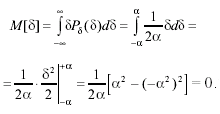(3.39)

Дисперсию случайной равномерно распределенной погрешности можно найти по формуле:

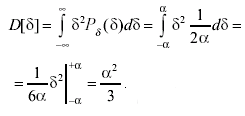(3.40)

Вероятность попадания случайной погрешности в заданный интервал (δ₁; δ₂] при равномерном распределении равна

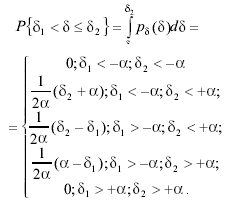(3.41)

На графике функции распределения эта вероятность равна заштрихованной на рис. 3.5 площади.

Если интервал изменения δ полностью укладывается внутри интервала изменения а, то искомая вероятность просто равна отношению длин этих интервалов. Если интервал изменения δ находится полностью за пределами интервала изменения α, то вероятность попадания случайной погрешности в интервал (δ₁; δ₂] равна нулю.

⇐ Предыдущая 1 2 345 Следующая ⇒