P1 = 132.6×500 = 66300Н = 66.3кН; P2 = 3×132.6×500 = 199000Н = 199кН; M1 = 2×132.6×5002 = 6.63×107 Н×мм = 66.3кН×м.

Напряжения: 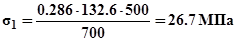; ; 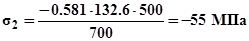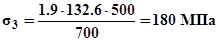, действующие в стержнях удовлетворяют условиям прочности.

Более сложная постановка задачи. (с учетом монтажных напряжений )

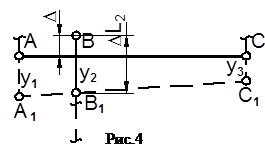Будем считать, что стержень №2 до сборки конструкции имел длину, отличающуюся от номинальной на малую величину D = 0.5 мм (знак “+” означает, что начальная длина стержня больше номинальной). Уравнения (1), (2), (3) останутся без изменений, изменится только зависимость между перемещением шарнира B и удлинением стержня №2: 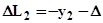, тогда уравнение совместности деформаций (4) перепишется в виде: 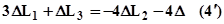, (смотри рис.4). Используя закон Гука, получим: 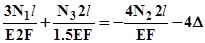, откуда выразим: 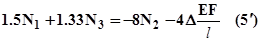. Решая совместно (1), (2), (5¢) выразим нормальные силы и напряжения в стержнях:

; ; .

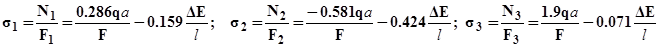Вычисляя величины вторых слагаемых в выражениях для напряжений (DE/l =200 МПа.):

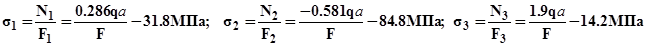убеждаемся, что монтажные напряжения не превосходят допускаемых и следовательно условие прочности при сборке конструкции не нарушается.

Очевидно, что стержень №2 сжат, из условия прочности второго стержня допускаемую внешнюю нагрузку, выраженную через q:

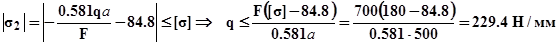
Стержни №1 и №3 могут оказаться как сжатыми, так и растянутыми, в зависимости от величины параметра внешней нагрузки – q,однако, проводя анализ (смотри предыдущую задачу)можно установить, что в любом случае напряжения сжатия в этих стержнях не превосходят соответственно31.8 МПа и 14.2 МПа. Следовательно, для стержней №1 и №3 достаточно записать только условия прочности на растяжение, кроме того, очевидно, что наибольшее растягивающее напряжение будет в стержне №3. Определим из условия прочности третьего стержня допускаемую внешнюю нагрузку, выраженную через q:

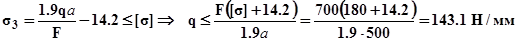
Учитывая, что должны выполнятся оба условия прочности, принимаем наименьшее значение q_max= 143.1 Н/мм. Тогда внешние силы будут равны:

⇐ Предыдущая 1 234 5 6 7 8 Следующая ⇒