класс. М3М1ч стр.8 №9. М1М1ч стр. 21 №8. М3М1ч стр.13 №8. М3М1ч стр.76 №9. М4М1ч стр.7 №17. М4М1ч1 стр. 36 №150. М4М1ч стр.64 №292

3 класс

М3М1ч стр.8 №9

Для того, чтобы проверить, что отрезки равны, выполним их измерение линейкой. Получим: 4см=4см.

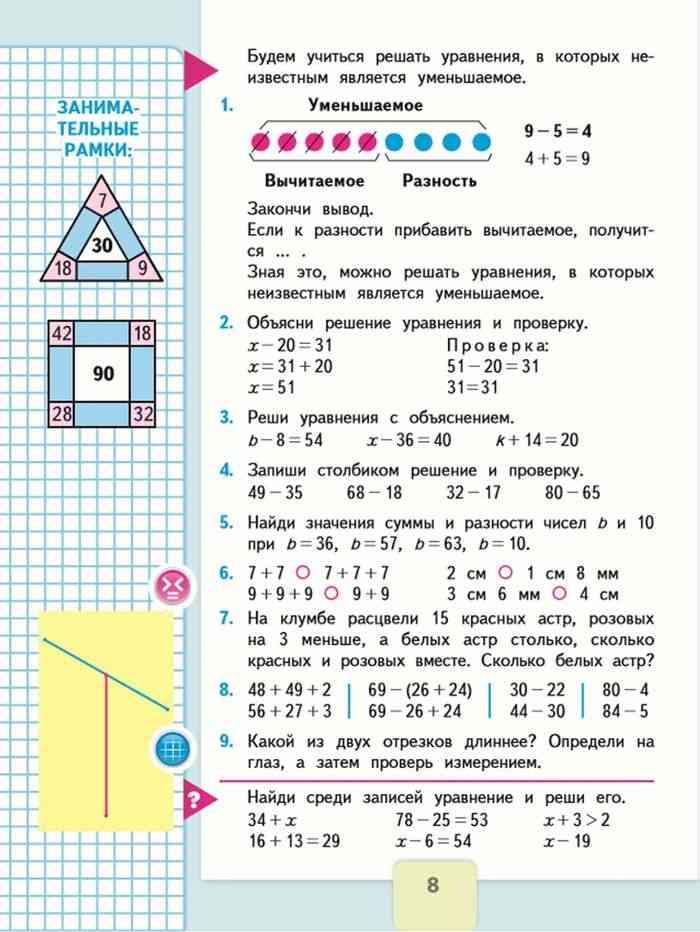
М1М1ч стр. 21 №8

Для того, чтобы доказать правильность наших вычислений, выполним проверку сложения вычитанием, а вычитания – сложением.

91-15=76 55+38=93 76-29=47 56+15=71

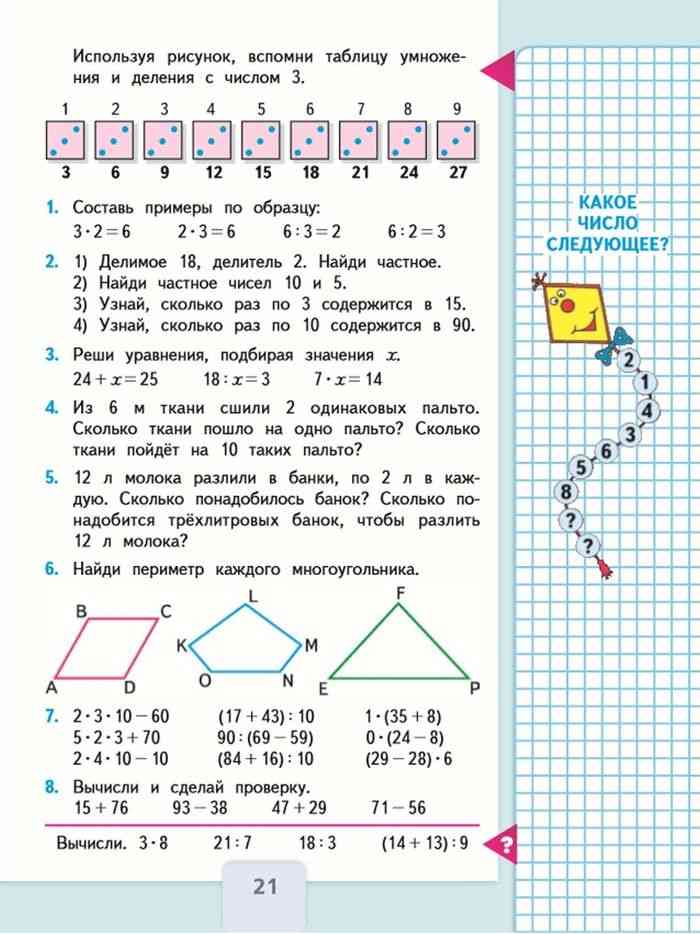
М3М1ч стр.13 №8

Здесь верны 2 высказывания: 1 и 2. Но для умозаключения нам необходимо лишь то, что касается зелёного цвета. Чтобы закончить фразу, построим дедуктивное умозаключение.

Все фигуры зелёного цвета не многоугольники. Фигура – зелёного цвета, значит она не многоугольник.

На основе данного умозаключения закончим высказывание:

Если фигура зелёного цвета, то она не многоугольник.

М3М1ч стр.76 №9

Для того, чтобы доказать, что из 1 2 4 и 1 3 4 можно сложить розовый прямоугольник в учебнике, построим такой же у себя в тетрадях и разобьём его на эти фигуры.

4 4 3

4 класс

М4М1ч стр.7 №17

Для доказательства правильности вычислений выполним проверку вычислением в столбик.

_972 +375 +608 _813

169 50 128 357

803 425 736 456

М4М1ч1 стр. 36 №150

Для того, чтобы доказать, что мы верно определили на глаз длину отрезков, выполним проверку, измерив их длину по линейке в миллиметрах. Получим:

АВ=30мм, СD=80мм, КМ=50мм.

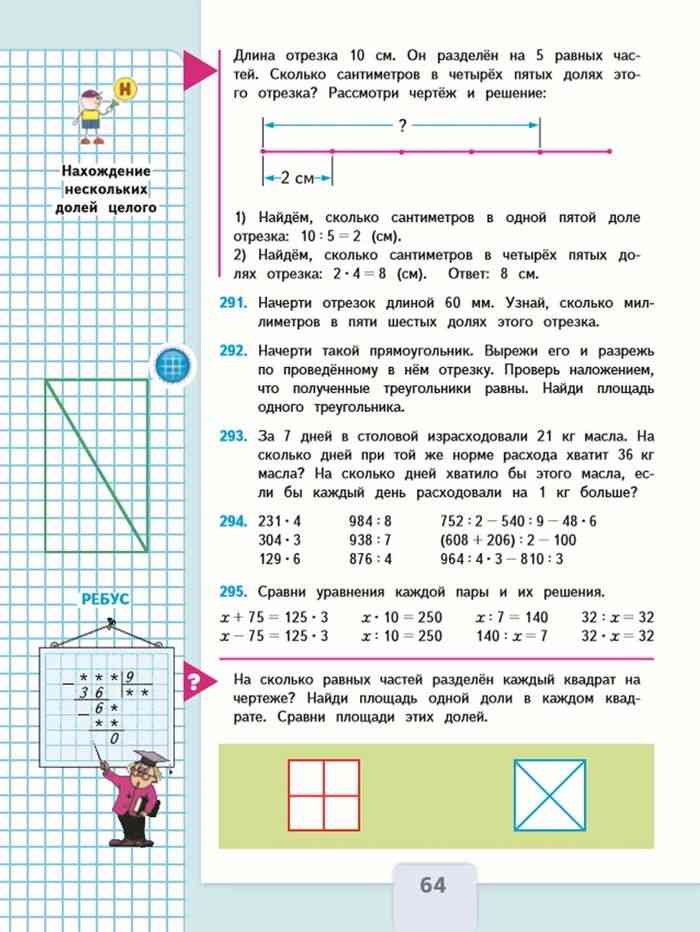
М4М1ч стр.64 №292

Чтобы доказать, что треугольники прямоугольника равны, начертим такой же прямоугольник у себя в тетрадях и разрежем по проведённому в нём отрезку на 2 треугольника, наложим их один на другой. Видим, что треугольники равны, значит у них одинаковая площадь.

⇐ Предыдущая 1 234 5 6 7 8 9 Следующая ⇒