М1М1ч стр.27 вверху. На дедуктивные умозаключения задачи не дают, т. к. детям это пока сложно, но уже идёт к ним подготовка.. М2М1ч стр.37 №5. М2М1ч стр.41 №1. М2М1ч стр. 93 №24. М2М2ч стр.86 №3

М1М1ч стр.27 вверху

Для того, чтобы доказать, что 1<2, 3>2, 3>1, посмотрим на модели слева и справа. Сравним треугольники в левом и кубики в правом столбиках с нашими записями в тетради. Видим, что 1зелёному треугольнику нет пары красного, значит 1 меньше 2. Видим, что у 3 синих треугольников нет 1 пары с зелёными, значит 3 больше 2. Видим, что 3 синим треугольникам не хватает 2 пар для красных, значит 3 больше 1.

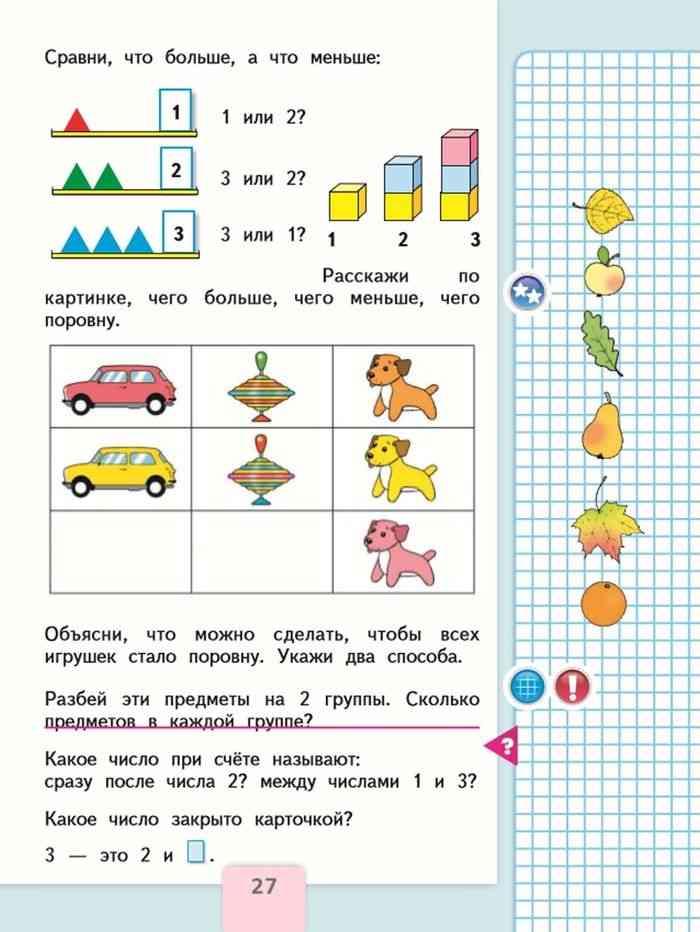
На дедуктивные умозаключения задачи не дают, т. к. детям это пока сложно, но уже идёт к ним подготовка.

2 класс

М2М1ч стр.37 №5

Для того, чтобы доказать, что красный и синий отрезки равны, а зелёный отрезок длиннее их обоих, выполним их измерение. Получаем: с.=3см кр.=3см з.=5см, следовательно 3=3 и 5>3, следовательно с.=кр. c.<з. кр.<з.

М2М1ч стр.41 №1

Для того, чтобы убедиться в правильности наших вычислений, сравним их с моделями над ними. Видим, что треугольникам не хватает 2 пар с белыми кругами, значит 3<5. Видим, что всем треугольникам хватает кругов, следовательно 8=8. Видим, синим кружкам не хватило 1 пары с красными, значит 4>3.

М2М1ч стр. 93 №24

Для того, чтобы проверить правильность вычислений, проверим сложение вычитанием, а вычитание – сложением.

73+7=80 93-30=63 38+40=78 30-4=26

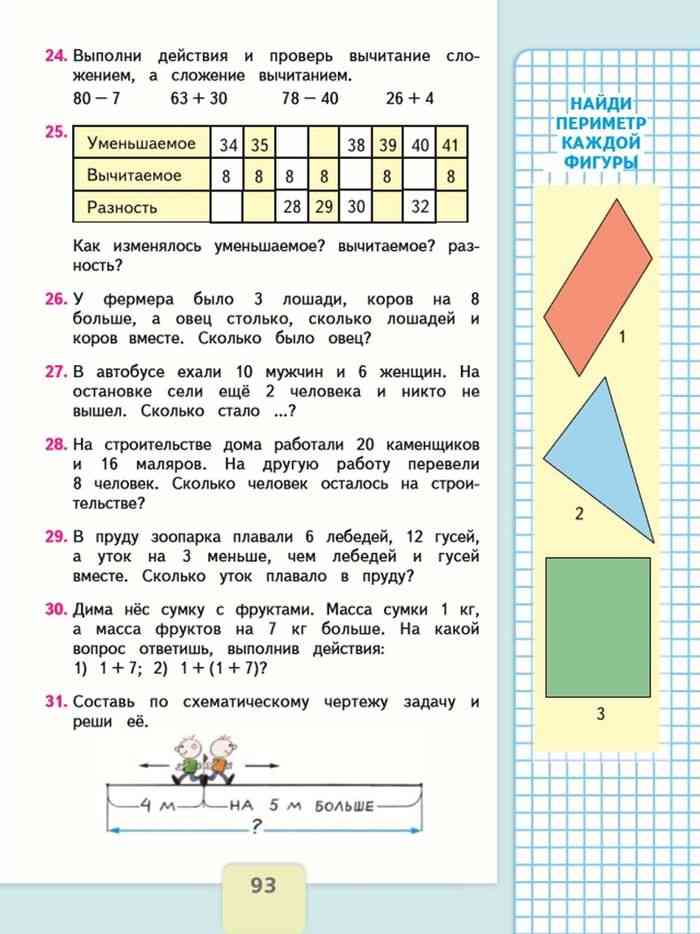
М2М2ч стр.86 №3

Для того, чтобы закончить высказывание, построим дедуктивное умозаключение.

Фигура жёлтого цвета – треугольник. Если фигура пятиугольник, то она не жёлтого цвета.

⇐ Предыдущая 123 4 5 6 7 8 9 Следующая ⇒