Какие способы доказательства истинности суждений вам известны? Приведите примеры таких доказательств в курсе математики начальных классов.

Вопрос 10

В начальных классах доступными являются следующие способы доказательства истинности суждений.

1) Измерение– получение результата измерением, может выступать результатом обоснования какого-либо единичного, частного суждения.

2) Вычисление– высказывание, утверждение можно проверить с помощью вычислений.

3) Эксперимент (моделирование) – высказывание, утверждение можно проверить с применением наглядности и предметных действий.

4) Дедуктивные умозаключения – основной способ доказательства истинности в математике.

Суть сводится к тому, что на основе общего суждения, о предмете данного класса и некоторого единичного суждения о каком-то предмете, высказывается новое единичное суждение о том же предмете.

Общее суждение – общая посылка.

1 единичное суждение – это частная посылка,

новое единичное суждение – умозаключение.

УМК «Школа России»

1 класс

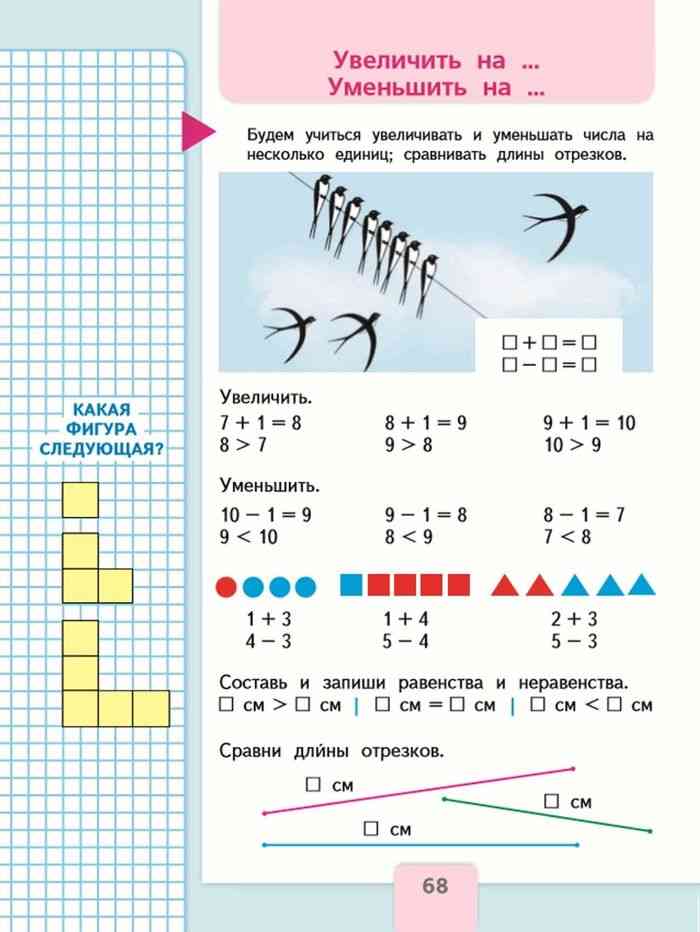
М1М1ч стр.68 внизу

Для доказательства того, что зелёный отрезок самый маленький, синий и красный – равны, проводим измерение длин отрезков по линейке. Получаем кр.=9см, с.=9см, з.=6см, следовательно, т. к. 9>6 и 9=9, то кр.=с. с.>з. кр.>з.

М1М1ч стр.120 №6

Для проверки правильности решения примеров, выполним вычисленияи сравним их с уже данными примерами. Если результат нашего вычисления совпадет с примером из учебника, то он решён верно, а если не совпадёт – неверно. Вычисляем:

6+3=9 8-3=5 0+3=3

7+2=9 9-2=7 1+0=1

Сравним наши результаты с данными из учебника:

9<10 5=5 3=3

9=9 6<7 10>1

Мы доказали, что 2,3 и 5 примеры решены правильно, а остальные – неправильно.

12 3 4 5 6 7 8 9 Следующая ⇒