Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Домашнее задание.. Метод координат

Домашнее задание.

1.В правильной четырехугольной пирамиде 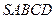с основанием 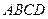сторона основания равна 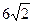, а боковое ребро равно 10. Найдите угол между плоскостям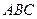и и 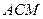, где точка 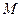делит ребро 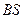так, что 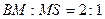Ответ: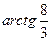

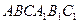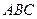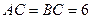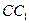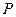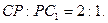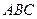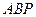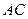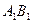2.Основанием прямой треугольной призмы является треугольник , в котором , а один из углов равен 60⁰. На ребре отмечена точка так, что  Найдите тангенс угла между плоскостями и , если расстояние между прямыми и равно 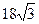. Ответ:4

3.В прямоугольном параллелепипеде 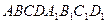известны ребра 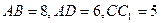. Найдите угол между плоскостям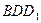и  и 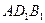.Ответ: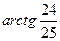

Метод координат

1. Нахождение угла между нормалями данных плоскостей.

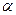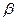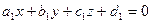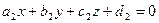Задачу о нахождении угла между плоскостями и , заданными уравнениями  и  соответственно, удобнее свести к задаче о нахождении угла между векторами их нормале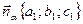й  и 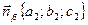, используя формулу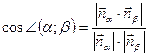

Пример

1.В кубе 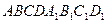 найти угол между плоскостями и .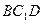

; ;  ; ; ;

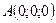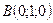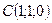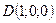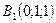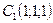
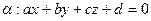
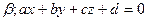
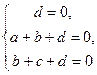
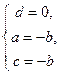
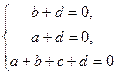
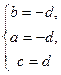
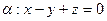
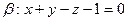
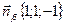
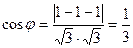; Ответ: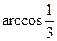

2. В правильной пирамиде 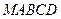(М – вершина) высота и сторона основания равны 4. Точка 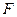- середина ребра 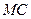. Плоскость 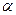проходит через середину ребра 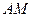перпендикулярно прямой 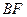. Найти угол между: а) плоскостью 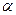и плоскостью основания; б) плоскостью 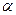и прямой .

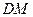Решение.

Так как 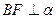, то 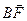- нормаль к плоскости 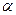, 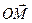- нормаль к плоскости .

;

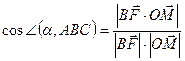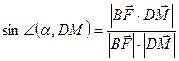
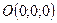
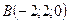
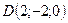
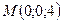
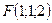
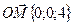
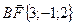
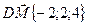
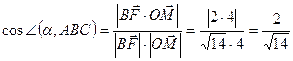
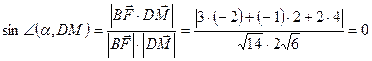
Ответ: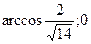

3. В единичном кубе 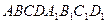 найти угол между плоскостям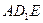и и 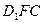, где точк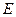и и 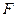- середины ребер 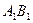и соответственно.

; ; ; ; ;

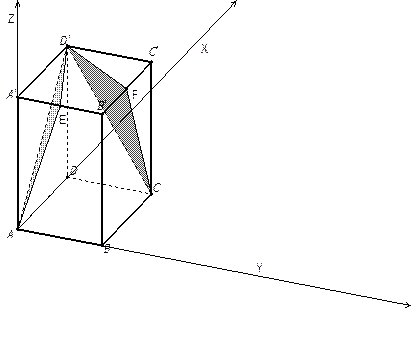
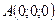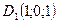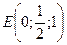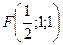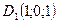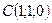
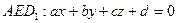
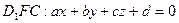
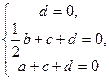
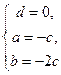
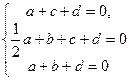
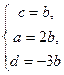
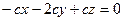
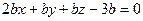
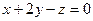
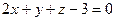
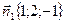
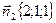
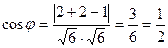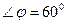; ; Ответ: 60⁰

4.Дан куб 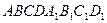. Найти угол между плоскостям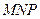и и 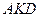, где точки 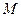- центр грани 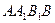, 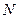- середина ребра 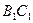, 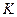- середина ребра 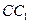, точка 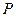- делит ребро 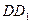в отношении .

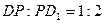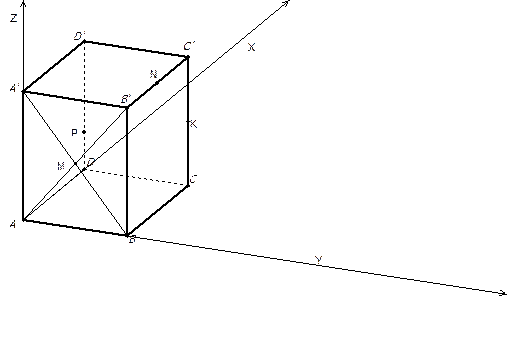
Проведите решение самостоятельно.

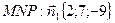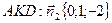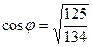; ; ; Ответ: