
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Угол между плоскостями в пространстве.
Угол между плоскостями в пространстве.
Определение1. Двугранным углом в пространстве называется фигура, образованная двумя полуплоскостями с общей граничной прямой.
Определение 2. Линейным углом двугранного угла называется угол, образованный лучами с вершиной на граничной прямой, стороны которого лежат на гранях двугранного угла и перпендикулярны граничной прямой.
Величиной двугранного угла называется величина его линейного угла.
Определение 3.Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.
Куб
Устно
1. В кубе 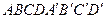 найдите угол между плоскостями
найдите угол между плоскостями 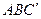 и
и 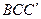 .
.
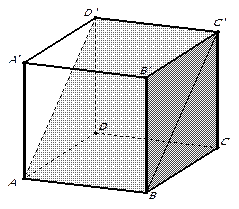
2. В кубе 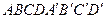 найдите угол между плоскостями
найдите угол между плоскостями 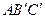 и
и 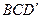 .
.
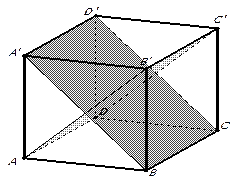
3. В кубе 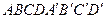 найдите угол между плоскостями
найдите угол между плоскостями 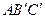 и
и 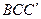 .
.
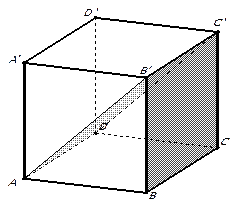
4. В правильной шестиугольной призме 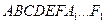 найдите угол между плоскостями
найдите угол между плоскостями 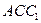 и
и 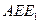

Работа в тетради
1.В кубе 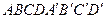 найдите тангенс угла между плоскостями
найдите тангенс угла между плоскостями 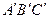 и
и 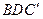 .
.

Решение.

Искомый угол 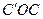 . Объясните почему?
. Объясните почему? 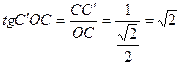 .
.
Далее три задачи разбираем устно, рисуя линейные углы на чертежах.
2. В кубе 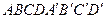 найдите тангенс угла между плоскостями
найдите тангенс угла между плоскостями 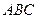 и
и 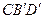 .
.
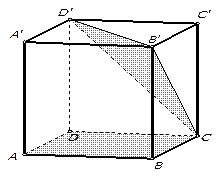
3. В кубе 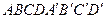 найдите тангенс угла между плоскостями
найдите тангенс угла между плоскостями 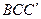 и
и 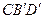 .
.
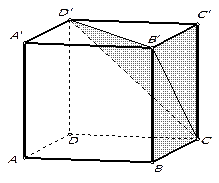
4. В кубе 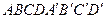 найдите тангенс угла между плоскостями
найдите тангенс угла между плоскостями  и
и 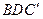 .
.
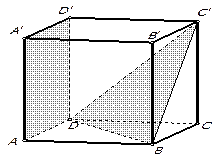
Ответы: 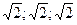 .
.
Почему ответы в этих трех задачах одинаковые.
Далее, работа в тетради.
5.В кубе 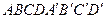 найдите тангенс угла между плоскостями
найдите тангенс угла между плоскостями 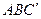 и
и 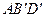 .
.
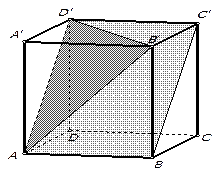
Ответ: 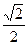 .
.
6.В кубе 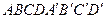 найдите косинус угла между плоскостями
найдите косинус угла между плоскостями 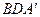 и
и 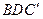 .
.

Решение.

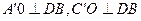 .
.
Каково положение точки О?
Рассматриваем 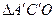 .
.
Находим все стороны этого треугольника.
По теореме косинусов по трем сторонам находим 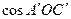 .
.
Ответ: 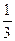
7. В кубе 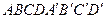 точки
точки 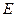 и
и 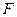 - середины ребер соответственно
- середины ребер соответственно 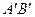 и
и 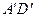 . Найдите тангенс угла между плоскостями
. Найдите тангенс угла между плоскостями 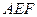 и
и 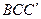 .
.
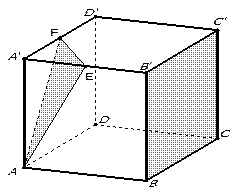
Решение.
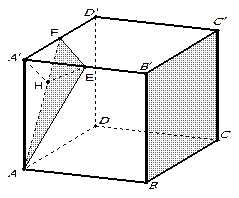
Прокомментируйте чертеж.
Искомый угол?
Какой 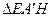 ?
?
Вычислите искомый угол?
Ответ: 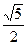
Домашнее задание:
1. В кубе 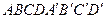 найдите косинус угла между плоскостями
найдите косинус угла между плоскостями 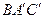 и
и 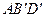 .
.

Ответ: 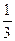
2. В кубе 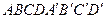 найдите угол между плоскостями
найдите угол между плоскостями 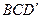 и
и 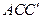 .
.

Ответ: 60
3. В кубе 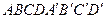 точки
точки 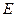 и
и 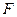 - середины ребер соответственно
- середины ребер соответственно 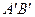 и
и 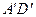 . Найдите тангенс угла между плоскостями
. Найдите тангенс угла между плоскостями 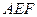 и
и 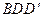 . Ответ:
. Ответ: 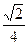
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|