
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вероятность события.
3. Вероятность события.
Пусть событие А связано с испытанием, имеющим n равновозможных элементарных исходов. И пусть событие A наступает тогда, когда осуществляется один из каких-то m элементарных исходов 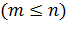 , и не наступает тогда, когда осуществляется любой из оставшихся (
, и не наступает тогда, когда осуществляется любой из оставшихся ( 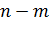 ) исходов. Тогда говорят, что указанные m исходов, приводящие к наступлению события A, благоприятствуют событию A.
) исходов. Тогда говорят, что указанные m исходов, приводящие к наступлению события A, благоприятствуют событию A.
Определение 5. Вероятностью P(A)события A в испытании с равновозможными элементарными исходами называется отношение числа исходов m благоприятствующих событию A, к числу n всех исходов испытания.
Таким образом, вероятность события A определяется по формуле:
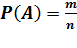 . (1)
. (1)
Здесь n – число всех исходов испытания, m – число исходов, благоприятствующих событию A, 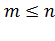 . Приведённое определение вероятности называютклассическим определением вероятности.
. Приведённое определение вероятности называютклассическим определением вероятности.
Обратите внимание, что в испытании с n равновозможными исходами вероятность наступления каждого элементарного события равна 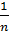 . Так, например, появление любого из шести чисел 1, 2, 3, 4, 5, 6 после одного бросания игрального кубика имеет вероятность
. Так, например, появление любого из шести чисел 1, 2, 3, 4, 5, 6 после одного бросания игрального кубика имеет вероятность 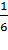 .
.
Из формулы (1) следует 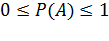 , а также P(V)=0, P(U)=1,
, а также P(V)=0, P(U)=1,
где V - невозможное событие; U – достоверное событие.
Задача №2:В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение.Общее число различных исходов есть n = 1000. Число исходов, благоприятствующих получению выигрыша, составляет m= 200. Согласно формуле 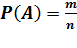 , получим
, получим 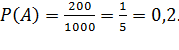
Ответ: 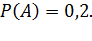
Задача №3:Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение.Обозначим событие, состоящее в появлении черного шара, через А. Общее число случаев есть n = 5 + 3. Число случаев m, благоприятствующих появлению события А, равно 3. По 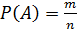 получим
получим 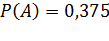
Ответ: 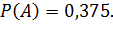
Задача №4:
Бросают две монеты. Найти вероятность события А - хотя бы на одной монете выпал орёл.
Решение.Обозначим появление орла на выпавшей монете буквой «О», а появление решки - «Р». Тогда равновозможны следующие четыре элементарных исхода испытания (n=4): ОО, РР, ОР и РО. Событию А благоприятствуют следующие 3 пары исходов : ОО, ОР и РО (m=3). Поэтому используя классическое определение вероятности имеем: 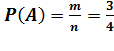 .
.
Ответ: 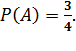
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|