Хелпикс

Главная

Контакты

Случайная статья



Пример 6(Несуществующий интеграл с бесконечным верхним пределом интегрирования).

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


Пример 6(Несуществующий интеграл с бесконечным верхним пределом интегрирования).

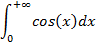
Подынтегральная функция 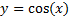 непрерывна на промежутке 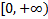, однако

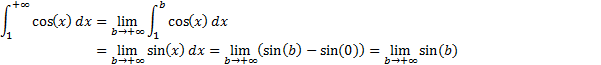
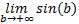 – не существует, поэтому несобственный интеграл расходится.

Пример 7 (Несуществующий интеграл с бесконечным нижним пределом интегрирования).

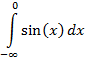
Подынтегральная функция 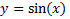 непрерывна на промежутке 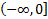, однако

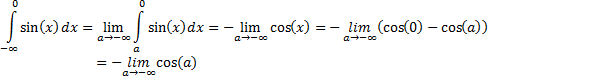
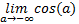 ­– не существует, поэтому несобственный интеграл расходится.

Интегралы с двумя бесконечными пределами интегрирования

1. Расписать интеграл как сумму интегралов, где попеременно верхний и нижний пределы в виде произвольного числа.

2. Вычислить неопределенный интеграл.

3. Вычислить сумму пределов

Пример 8(Сходящийся интеграл с бесконечными пределами интегрирования).

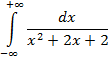
Подынтегральная функция 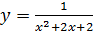 непрерывна на всей числовой оси

 

 

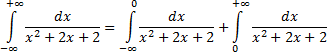
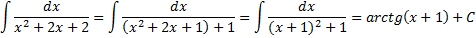
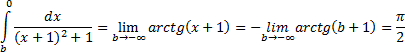
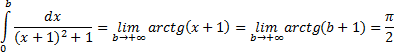
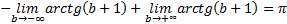
Интеграл сходится.

Пример 9(Сходящийся интеграл с бесконечными пределами интегрирования).

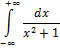
Подынтегральная функция 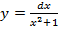 непрерывна на всей числовой оси

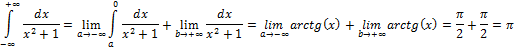
Интеграл сходится.

Интегралы 2 рода

1. Проверить пределы интегрирования на точки разрыва

2. Вычислить неопределенный интеграл

3. Определить стремление выражения

4. Вычислить предел с помощью формулы Ньютона-Лейбница

5. Определить сходимость или расходимость интегралов


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.