Хелпикс

Главная

Контакты

Случайная статья



Сходимость и расходимость интегралов

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒


Сходимость и расходимость интегралов

При вычислении несобственных интегралов необходимо охарактеризовать подынтегральную функцию: непрерывна она на промежутке интегрирования или нет.Это необходимо для идентификации типа несобственного интеграла.

Существуют признаки сходимости несобственных интегралов.

Признак сравнения.

Пусть для всех 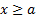 функци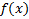и  и 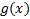 определены и выполняются неравенства 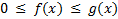. Тогда:

1. если 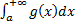 сходится, то и  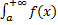сходится

2. если 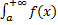 расходится, то и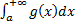

3. есл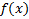и  и 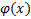 непрерывны и неотрицательны на промежутке  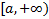(а также сохраняют свой знак на всем промежутке), причем 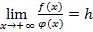, где 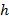 – действительное число, отличное от нуля , то интегралы  и 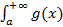 ведут себя одинаково относительно их сходимости

Решение

Рассмотрим примеры:

Интегралы 1 рода:

1. Проверить непрерывность функции

2. Вычислить неопределенный интеграл

3. Вычислить предел с помощью формулы Ньютона-Лейбница

4. Определить сходимость или расходимость интеграла

Пример 1(Расходящийся интеграл с бесконечным верхним пределом интегрирования).

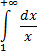
Подынтегральная функция  непрерывна на промежутке

Интеграл расходится.

Пример 2(Сходящийся интеграл с бесконечным верхним пределом интегрирования).

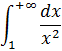
Подынтегральная функция  непрерывна на промежутке

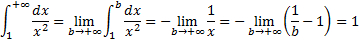
Интеграл сходится.

Пример 3(Расходящийся интеграл с бесконечным верхним пределом интегрирования).

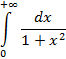
Подынтегральная функция 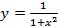 непрерывна на промежутке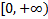

Интеграл расходится.

Пример 4(Сходящийся интеграл с бесконечным нижним пределом интегрирования).

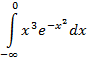
Подынтегральная функция  непрерывна на промежутке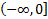

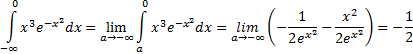
Интеграл сходится.

Пример 5(Расходящийся интеграл с бесконечным нижним пределом интегрирования).

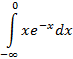
Подынтегральная функция 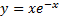 непрерывна на промежутке (-∞,0]

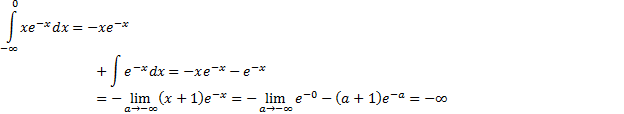
Интеграл расходится.

 


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.