
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 4.. Решение.
Рис. 2
Пример 4.
Консольная балка прямоугольного поперечного сечения с соотношением сторон 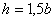 нагружена в вертикальной и в горизонтальной плоскостях сосредоточенными силами
нагружена в вертикальной и в горизонтальной плоскостях сосредоточенными силами 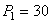 кН,
кН, 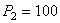 кН, сосредоточенным моментом
кН, сосредоточенным моментом 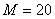 кНм и равномерно распределённой нагрузкой интенсивностью
кНм и равномерно распределённой нагрузкой интенсивностью  кН/м (рис. 1).
кН/м (рис. 1).
Определить рациональную ориентацию поперечного сечения (ребром или плашмя), а также его размеры b и h из условия прочности при допускаемом нормальном напряжении 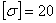 кН/см2. Построить эпюру нормальных напряжений по контуру опасного поперечного сечения.
кН/см2. Построить эпюру нормальных напряжений по контуру опасного поперечного сечения.
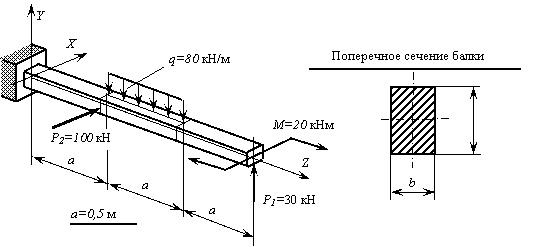
Рис. 1
Решение.
Для прямоугольного поперечного сечения условие прочности при одновременном изгибе в двух плоскостях можно записать в виде:
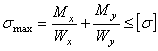 ,
,
где 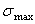 – максимальное значение нормального напряжения, возникающего в поперечном сечении балки;
– максимальное значение нормального напряжения, возникающего в поперечном сечении балки; 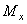 и
и 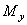 – изгибающие моменты;
– изгибающие моменты; 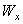 и
и 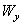 – осевые моменты сопротивления поперечного сечения относительно главных центральных осей x и y соответственно.
– осевые моменты сопротивления поперечного сечения относительно главных центральных осей x и y соответственно.
1. Строим эпюры изгибающих моментов 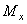 и
и 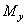 по значениям, вычисленным для характерных сечений (рис. 2).
по значениям, вычисленным для характерных сечений (рис. 2).
Воспользуемся принципом суперпозиции и сначала рассмотрим изгиб балки в вертикальной плоскости.
Сечение 1:
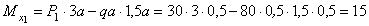 кНм.
кНм.
Сечения 2 и 3:
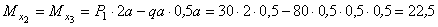 кНм.
кНм.
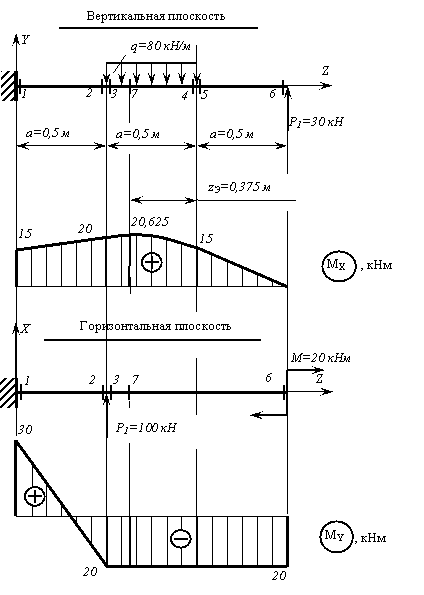
Рис. 2
Сечения 4 и 5:
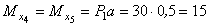 кНм.
кНм.
Сечение 6:
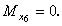
На участке балки, нагруженном равномерно распределённой нагрузкой интенсивностью q, необходимо сделать дополнительное сечение 7. Перерезывающая сила 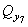 , возникающая в этом сечении, равна
, возникающая в этом сечении, равна
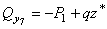
и при 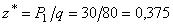 м она обращается в нуль.
м она обращается в нуль.
Следовательно, в этом поперечном сечении балки изгибающий момент 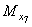 принимает экстремальное значение:
принимает экстремальное значение:
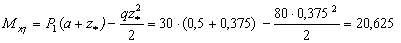 кНм.
кНм.
Теперь рассмотрим изгиб балки в горизонтальной плоскости.
Сечение 1:
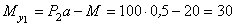 кНм.
кНм.
Сечения 2 –7:
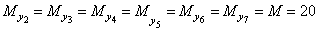 кНм.
кНм.
2. Определяем необходимые размеры поперечного сечения балки при егорасположении ребром.
Осевые моменты сопротивления равны:
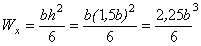 ;
; 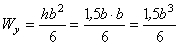 .
.
Условие прочности принимает вид:
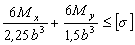
Отсюда, после несложных преобразований,
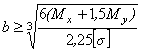 .
.
Отметим, что при косом изгибе расположение опасного с точки зрения прочности сечения не всегда очевидно. Поэтому нам необходимо исследовать несколько сечений, «похожих» на опасные сечения.
Сечение 1:
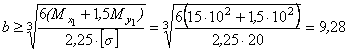 см.
см.
Сечение 7:
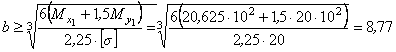 см.
см.
Из двух полученных выше значений размера b нам следует выбрать большее значение. Таким образом, для случая расположения балки ребром принимаем следующие размеры поперечного сечения:
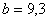 см;
см; 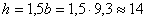 см.
см.
3. Теперь определим необходимые размеры поперечного сечения балки при ее расположении плашмя.
Осевые моменты сопротивления в этом случае равны:
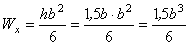 ;
; 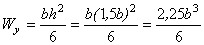 .
.
Условие прочности принимает вид:
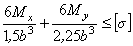 .
.
Отсюда
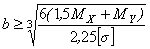 .
.
Из условия прочности сечения 1 получим:
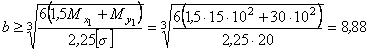 см,
см,
а из условия прочности сечения 7 –
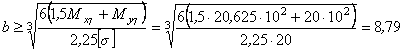 см.
см.
Из двух найденных выше значений принимаем для размера b большеезначение: 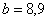 см. Тогда
см. Тогда
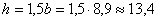 см.
см.
Анализируя полученные результаты, видим, что расположение поперечного сечения балки плашмяявляется более рациональным, поскольку в этом случае размер 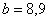 смоказываетсяменьше, чем при расположении балки ребром (
смоказываетсяменьше, чем при расположении балки ребром ( 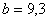 см).
см).
4. Строим эпюру нормальных напряжений по контуру опасного сечения1. Осевые моменты сопротивления:
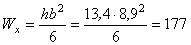 см
см 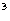 ;
; 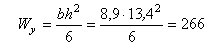 см
см 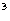 .
.
Максимальные значения нормальных напряжений при изгибе в вертикальной и горизонтальной плоскостях соответственно равны:
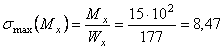 кН/см
кН/см 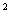 ;
;
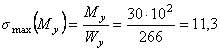 кН/см
кН/см 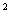 .
.
Эпюры 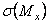 и
и 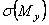 от изгиба в вертикальной и горизонтальной плоскостях соответственно представлены на рис. 3.
от изгиба в вертикальной и горизонтальной плоскостях соответственно представлены на рис. 3.
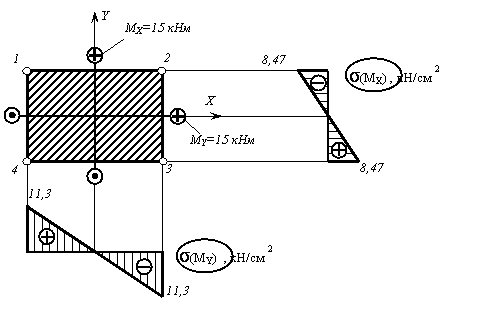
Рис. 3
Определяем значения напряжений в угловых точках поперечного сечения с учётом их знака:
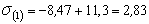 кН/см
кН/см 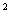 ;
; 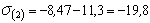 кН/см
кН/см 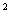 ;
;
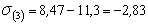 кН/см
кН/см 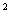 ;
; 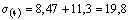 кН/см
кН/см 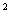 .
.
Эпюра нормальных напряжений 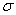 по контуру поперечного сечения, расположенного плашмя, представлена на рис. 4.
по контуру поперечного сечения, расположенного плашмя, представлена на рис. 4.

Рис. 4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|