
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 3.. Решение.
Рис. 3
Найдем угол 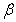 (см. рис. 3) между нейтральной линией и осью
(см. рис. 3) между нейтральной линией и осью 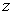 :
:
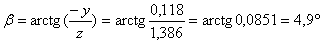
Отложим в масштабе найденные ранее вертикальную 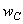 и горизонтальную
и горизонтальную 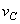 составляющие перемещения с учетом их направления. Полное перемещение точки
составляющие перемещения с учетом их направления. Полное перемещение точки 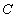 – отрезок
– отрезок 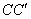 на рис. 3 равен геометрической сумме
на рис. 3 равен геометрической сумме 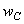 и
и 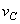 . Угол
. Угол 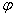 между полным перемещением и осью
между полным перемещением и осью 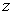
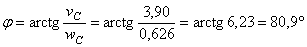 .
.
Таким образом, угол между полным перемещением 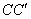 и нейтральной линией
и нейтральной линией 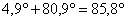 , что близко к
, что близко к  .
.
Пример 3.
Для стержня (рис. 1) определить внутренние силовые факторы в произвольном поперечном сечении и их построить эпюры.
Дано: F1 = 100 Н, F2 = 300 Н, q = 75 Н/м, a = 0, 3 м, b = 0, 2 м, l = 2 м.
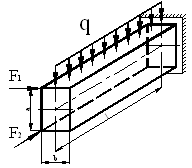
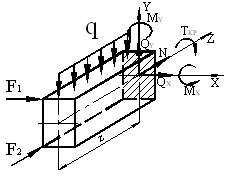
а) б)
Рис. 1
Решение.
Рассекаем брус на произвольном расстоянии z от его свободного конца. Отбрасываем правую часть. Располагаем оси координат в центре тяжести сечения. Действие правой части бруса на его левую часть заменяем внутренними силами: N, Qx, Qy, Mx, My, Ткр (рис. 1, б).
Уравновешиваем, то есть, записываем уравнения равновесия и определяем значения внутренних силовых факторов.
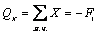 ;
;
QX = - 100Н.
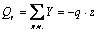 ;
;
при z = 0 Qy = 0;
при z = l Qy = -150 Н.
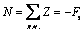 ;
;
N = - 300Н.
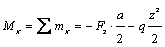 ;
;
при z = 0 Mx = - 45 Нм;
при z = l Mx = -195 Нм.
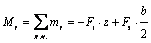 ;
;
при z = 0 My = 30 Нм; при z = l My = - 170 Нм.
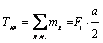 ; Ткр = 15 Нм.
; Ткр = 15 Нм.
Строим эпюры внутренних силовых факторов (рис. 2). Опасное сечение в данном брусе будет находиться в заделке, так как в этом сечении значения всех внутренних силовых факторов имеют наибольшие величины.
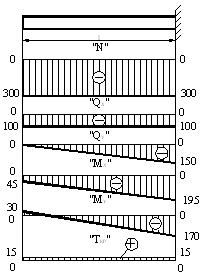
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|