
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Развертки поверхностей
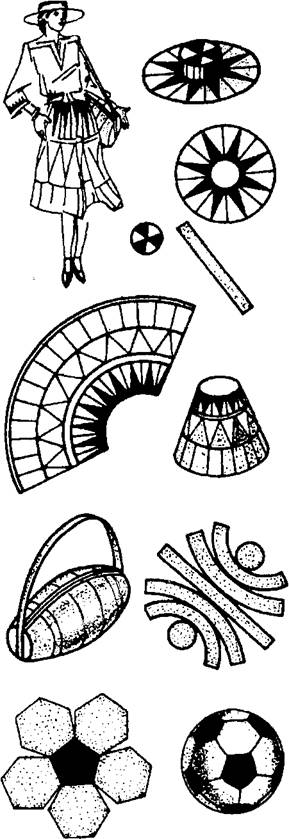
Каждый из нас ежедневно использует вещи, изготовленные по их разверткам: платья, блузы, юбки, брюки, сумки, портфели, обувь, перчатки, куртки; по разверткам изготовляют мячи футбольные, волейбольные, упаковку - для телевизоров, мониторов, подарочных духов и т. д.
Построение разверток (выкроек) поверхностей имеет большое практическое значение, так как является важнейшим технологическим этапом в тех видах производства, которые связаны с листовыми материалами: легкая промышленность (швейная, меховая, кожевенная и др. ), нефтехимическая и газовая (резервуары и трубопроводы из высококачественной листовой стали); судостроение, авто- и авиастроение; котлостроение; производство изделий из жести (водосточные трубы домов, воздуховоды и вытяжки в цехах и лабораториях... ) и т. д.
Развертки изделий выполняются на стадии проектирования.
В идеальном случае поверхность изделия совме
щается с плоскостью без растяжения и сжатия. Фи
гура, полученная в результате такого совмещения,
называется разверткой. .
Без растяжения и сжатия можно совместить с плоскостью, не получив ни складок, ни разрывов, поверхности только нескольких видов геометрических тел: многогранников (в том числе призм и пирамид), цилиндров и конусов. Такие развертки называют точными.
Однако для поверхностей цилиндров и конусов нередко строят и приближенные развертки. В этих случаях исходные поверхности заменяют более простыми - поверхностями призм или пирамид, развертки которых строить в ряде случаев легче (а точность практически остается достаточной).
Для всех других поверхностей (сфера, тор и др. ) строят условные развертки. Их точность не столь высока; здесь возможно использование растяжения или сжатия (механическим, температурно-влажностным и др. воздействием).
При построении разверток остаются неизменными метрические величины объектов - их длины, углы, площади и т. п.
На уроках математики, труда, технологии вы уже строили развертки для изготовления несложных предметов. Поэтому мы уверены, что решение задач, предложенных на следующих страницах, не вызовет у вас сложностей, но будет полезно для каждого.
Развертки поверхностей
Развертки поверхностей простейших геометрических тел
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|