
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задачи 6. Решение задачи 7. Решение задачи 8
Решение задачи 6
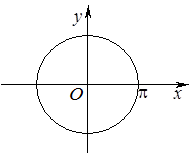 В случае, когда область D является частью круга или кольца, чаще всего удобно перейти к полярной системе координат (см. лекцию 14 ЛАиАГ). Связь между декартовыми и полярными координатами осуществляется согласно формулам (63) (ЛАиАГ). В данной ситуации область D – круг радиуса p, и намерение перейти к полярным координатам вызвано значительным упрощением описания этой области системой неравенств в полярных координатах по сравнению с декартовыми:
В случае, когда область D является частью круга или кольца, чаще всего удобно перейти к полярной системе координат (см. лекцию 14 ЛАиАГ). Связь между декартовыми и полярными координатами осуществляется согласно формулам (63) (ЛАиАГ). В данной ситуации область D – круг радиуса p, и намерение перейти к полярным координатам вызвано значительным упрощением описания этой области системой неравенств в полярных координатах по сравнению с декартовыми: 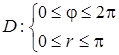 . Выразим подынтегральную функцию через полярные координаты:
. Выразим подынтегральную функцию через полярные координаты:
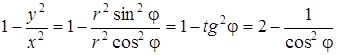 .
.
Для вычисления двойного интеграла в полярных координатах воспользуемся формулой (50) (см. также П. 47):
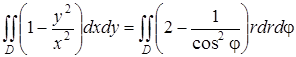
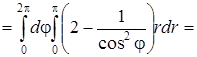
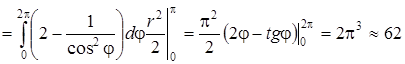 .
.
Решение задачи 7
Сделаем чертёж и далее будем действовать как в примере 48.
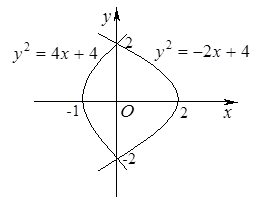 Центр тяжести данной фигуры определим по формулам (54), которые, в силу того, что плотность постоянна, приобретают вид:
Центр тяжести данной фигуры определим по формулам (54), которые, в силу того, что плотность постоянна, приобретают вид: 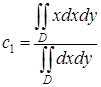 ,
, 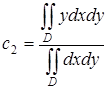 . Следует также заметить, что полученная фигура симметрична относительно оси Ох, из чего можно сделать вывод, что
. Следует также заметить, что полученная фигура симметрична относительно оси Ох, из чего можно сделать вывод, что 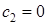 .
.
Найдём значение 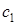 . Опишем область D, как область второго типа:
. Опишем область D, как область второго типа: 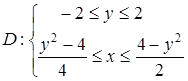
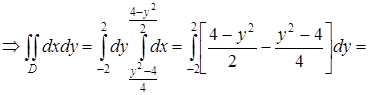
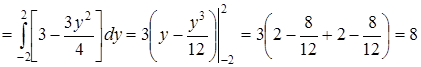 ;
;
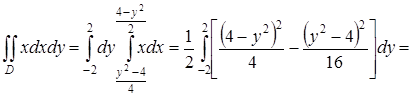
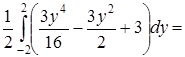
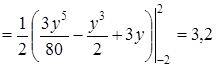 . Согласно формулам (54)
. Согласно формулам (54) 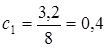 .
.
Решение задачи 8
Одно из приложений двойного интеграла – возможность вычисления объёма тела, боковой поверхностью которого является цилиндрическая поверхность (см. лекцию 15 ЛАиАГ). Например, если образующие этого тела параллельны оси Оz, основание D лежит в плоскости хОу, а сверху тело ограничено поверхностью 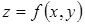 , то искомый объём вычисляется по формуле:
, то искомый объём вычисляется по формуле: 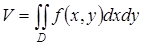 .
.
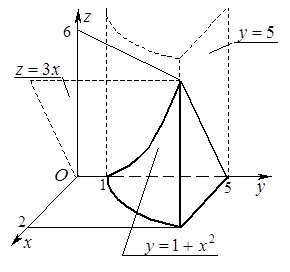 Как следует из чертежа, полученное тело удовлетворяет всем условиям для применения записанной формулы: сверху оно ограничено плоскостью
Как следует из чертежа, полученное тело удовлетворяет всем условиям для применения записанной формулы: сверху оно ограничено плоскостью 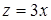 ; боковую поверхность образуют параболический цилиндр
; боковую поверхность образуют параболический цилиндр 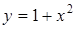 и плоскость
и плоскость 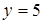 параллельные оси Оz; основание D лежит в плоскости
параллельные оси Оz; основание D лежит в плоскости 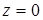 .
.
Опишем область D системой неравенств: 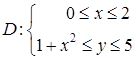 . Тогда
. Тогда
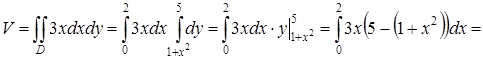
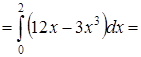
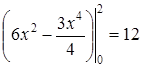 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|