
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1. Задача 2. Задача 3. Задача 4. Задача 5. Задача 6. Задача 7. Задача 8. Задача 9. РЕШЕНИЕ ЗАДАЧ. Решение задачи 1
ОБРАЗЕЦ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ПО ОПРЕДЕЛЁНЫМ, КРАТНЫМ И КРИВОЛИНЕЙНЫМ ИНТЕГРАЛАМ
Задача 1
Вычислить определённые интегралы:
1) 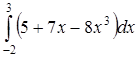 ; ;
| 2) 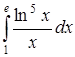 ; ;
| 3) 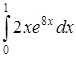 . .
|
Задача 2
Вычислить площадь фигуры, ограниченной линиями:
1) 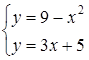 ; ;
| 2) 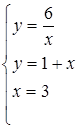 . .
|
Задача 3
Вычислить объёмы тел вращения:
1) 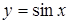 ,
, 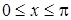 , вокруг оси Ох;
, вокруг оси Ох;
2) 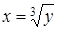 ,
, 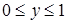 , вокруг оси Оу.
, вокруг оси Оу.
Задача 4
Вычислить длину дуги плоской кривой: 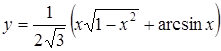 ,
, 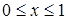 .
.
Задача 5
Вычислить с помощью двойного интеграла площади плоских фигур, ограниченных линиями:
1) 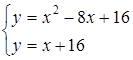 ; ;
| 2) 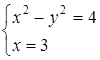 . .
|
Задача 6
Переходя к полярным координатам, вычислить двойной интеграл 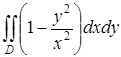 , где D :
, где D : 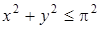 .
.
Задача 7
Вычислить координаты центра тяжести плоской фигуры, ограниченной линиями: 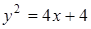 ,
, 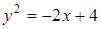 (плотность
(плотность 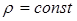 ).
).
Задача 8
Вычислить объём тела, ограниченного поверхностями: 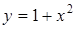 ;
; 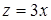 ;
; 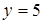 ;
; 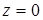 и расположенного в первом октанте.
и расположенного в первом октанте.
Задача 9
Вычислить криволинейный интеграл 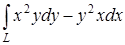 , где L – дуга кривой
, где L – дуга кривой 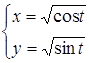 и
и 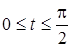 .
.
РЕШЕНИЕ ЗАДАЧ
Решение задачи 1
1) Для вычисления интеграла применим формулу Ньютона-Лейбница (22) и свойство линейности определённого интеграла (см. также П. 25):
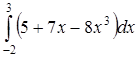
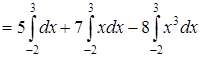
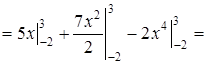
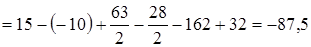 .
.
2) Здесь необходимо использовать метод замены переменной и применить формулу (23) (см. также П. 26):
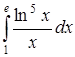
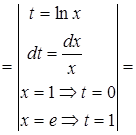
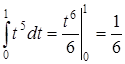 .
.
3) Для вычисления этого интеграла применим метод интегрирования по частям, то есть формулу (24) (см. также П. 27):
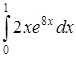
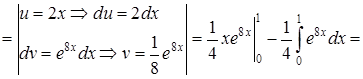
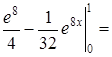
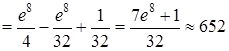 .
.
Решение задачи 2
1) Вычислим площадь фигуры с помощью формулы (26) (см. также П. 29), для применения которой сначала нужно построить графики заданных функций. Первая линия является параболой, а вторая – прямой. Найдём их общие точки, решив систему уравнений:
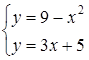
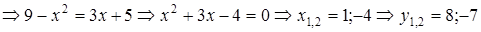 .
. 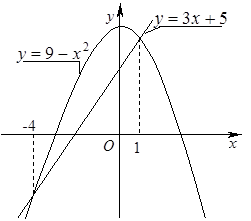
Таким образом в формуле (26) 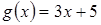 ,
, 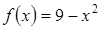 ,
, 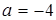 ,
, 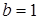 . Имеем:
. Имеем:

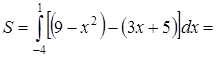
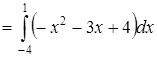
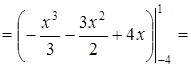
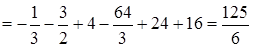 .
.

2) 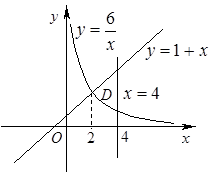
 Для нахождения площади этой фигуры будем действовать аналогично:
Для нахождения площади этой фигуры будем действовать аналогично: 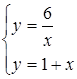
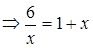
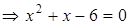
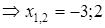
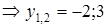 .
.
Проекция фигуры D, ограниченной заданными линиями, на ось Ох – отрезок 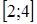 . То есть
. То есть 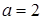 ,
, 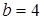 ,
, 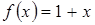 ,
, 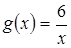 . Применим формулу (26):
. Применим формулу (26):
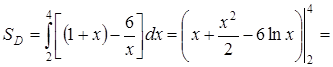
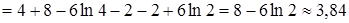 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|