
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задачи 3. Решение задачи 4. Решение задачи 5
Решение задачи 3
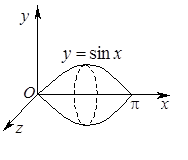
1) Для вычисления объёма тела вращения воспользуемся формулой (28) (см. также П. 30):
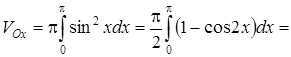
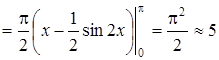 .
.
2) Здесь вращение линии происходит вокруг оси Оу, вследствие чего применяем формулу (29) (см. также П. 31):
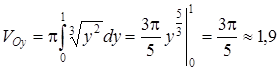 .
.
Решение задачи 4
Кривая задана в декартовых координатах, поэтому будем использовать формулу (31) (см. также П. 32). Сначала находим подынтегральную функцию:
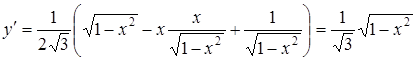 .
.
Таким образом подкоренное выражение примет вид:
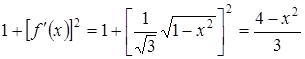 .
.
Тогда
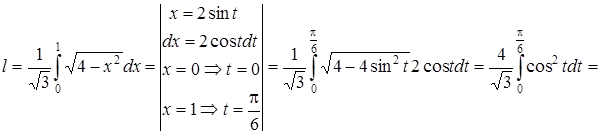
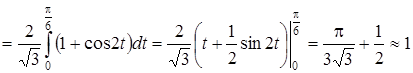 .
.
Решение задачи 5
Запишем свойство нормировки для двойного интеграла: 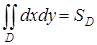 . Применим его для вычисления площади
. Применим его для вычисления площади 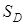 плоской фигуры D с помощью двойного интеграла.
плоской фигуры D с помощью двойного интеграла.
1) Чтобы использовать свойство нормировки, нужно построить фигуру D, описать её системой неравенств и перейти к повторному интегралу.
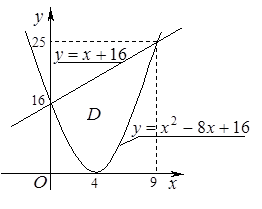 Для нахождения точек пересечения параболы и прямой решим систему уравнений:
Для нахождения точек пересечения параболы и прямой решим систему уравнений: 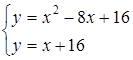
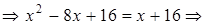
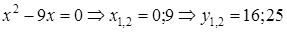 . Полученная фигура D является областью 1-го типа
. Полученная фигура D является областью 1-го типа 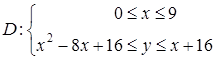 , поэтому при переходе к повторному интегралу будем использовать формулу (46):
, поэтому при переходе к повторному интегралу будем использовать формулу (46):
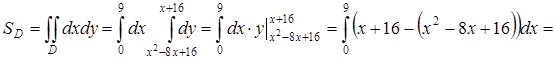
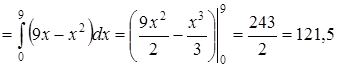 .
.
2) Одна из линий, ограничивающих фигуру D, является гиперболой с полуосями 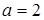 и
и 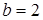 (см. лекцию 13 по ЛАиАГ). Другая линия – прямая, график которой расположен в полуплоскости положительных значений переменной х. Поэтому изобразим лишь одну ветвь гиперболы.
(см. лекцию 13 по ЛАиАГ). Другая линия – прямая, график которой расположен в полуплоскости положительных значений переменной х. Поэтому изобразим лишь одну ветвь гиперболы.
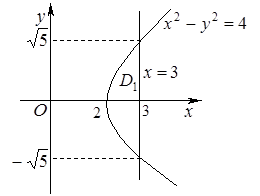 Фигура D симметрична относительно оси Ох и площадь её равна удвоенной площади фигуры
Фигура D симметрична относительно оси Ох и площадь её равна удвоенной площади фигуры 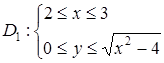
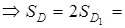
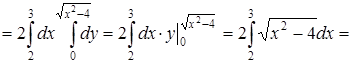
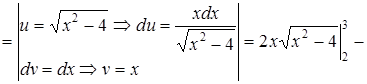
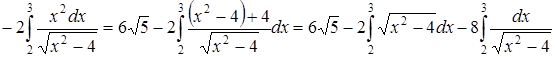 .
.
Следовательно,
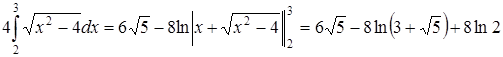
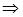
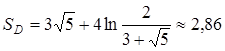 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|