Теорема. Пусть плоскости и пересекаются по прямой р. Плоскость параллельна прямой р. Тогда она пересекает плоскости и по прямым, параллельным .

Теорема. Пусть плоскости и пересекаются по прямой р. Плоскость параллельна прямой р. Тогда она пересекает плоскости и по прямым, параллельным.

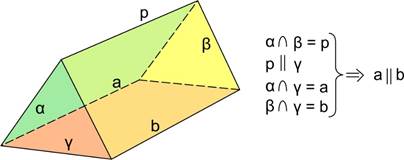
Как ее назвать? Для себя (не для оформления на экзамене! ) можно запомнить эту картинку как «домик» или «книжечку». Главное — запомнить формулировку и увидеть, как теорема применяется в решении задач.

Решить задачи:

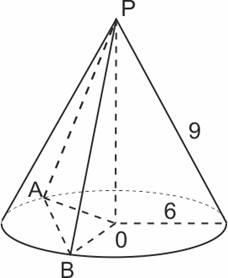
1. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1: 5. Найдите площадь сечения конуса плоскостью ABP.

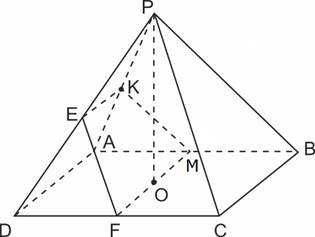
2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 6, точка K ― середина бокового ребра AP.

а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной плоскости BCP.

б) Найдите угол между плоскостью сечения и плоскостью основания пирамиды.

⇐ Предыдущая 1 23