Письменно ответить на вопросы:

Плоскость в пространстве. Плоскость можно провести через…
Расположение плоскостей в пространстве. Если две плоскости имеют общую точку, то они…
Расположение прямых в пространстве. Три случая.
Параллельность прямой и плоскости. Определение. Признак.
Что такое наклонная и проекция наклонной. Рисунок.
Угол между прямой и плоскостью.
Перпендикулярность прямой и плоскости. Определение. Признак.
Скрещивающиеся прямые. Угол между скрещивающимися прямыми. Расстояние между скрещивающимися прямыми (3 определения для расстояния между скрещивающимися прямыми).
Расстояние от прямой до параллельной ей плоскости – это…
Угол между плоскостями.
Параллельность плоскостей. Определение и признак.
Перпендикулярность плоскостей. Определение и признак.
Линии пересечения двух параллельных плоскостей третьей плоскостью…
Отрезки параллельных прямых, заключенные между параллельными плоскостями…
Теорема о трех перпендикулярах.

Сделать конспект «Прямоугольное проецирование и площадь проекции фигуры».

1. В задачах по геометрии успех зависит не только от знания теории, но от качественного чертежа. С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.

Как это сделать? Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.

Возьмем объемное тело. Выберем плоскость проекции. Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.

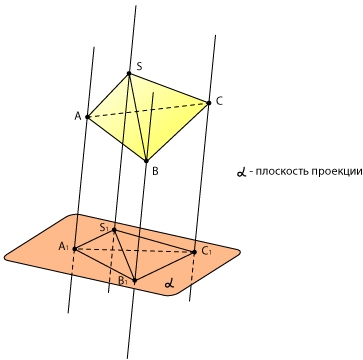
Как строить проекции объемных тел? Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:

Проекцией отрезка будет отрезок.

Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.

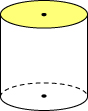
Проекцией круга в общем случае окажется эллипс.

Проекцией прямоугольника — параллелограмм.

Вот как выглядит проекция куба на плоскость:

Здесь передняя и задняя грани параллельны плоскости проекции

Можно сделать по-другому:

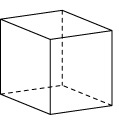
Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.

Рисуем проекции пирамиды,

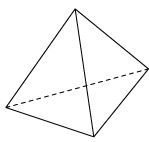
цилиндра:

и шара:

Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.

Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.

Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.

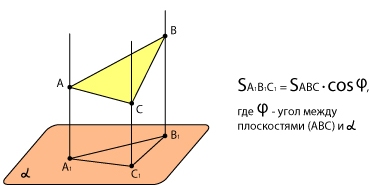
С помощью формулы для прямоугольной проекции фигуры можно находить угол между плоскостями.

2. Вот две важнейшие теоремы.

Есть множество ситуаций, когда без этой важнейшей теоремы не обойтись. Например, когда вам нужно построить сечение пирамиды плоскостью, параллельной одному из ребер основания. Такая задача была на ЕГЭ-2019.

Теорема о прямой и параллельной ей плоскости:

12 3 Следующая ⇒