
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
10. Какова вероятность того, что корни квадратного уравнения x2 + 2bx + c = 0 действительны?
7. По трём прямолинейным дорогам с постоянными скоростями идут три пешехода. В начальный момент времени они не находились на одной прямой. Докажите, что они могут оказаться на одной прямой не более двух раз.
Решение
Поставим каждому из пешеходов в соответствие точку в прямоугольной системе координат. Точки (х1; у1), (х2; у2), (х3; у3) лежат на одной прямой тогда и только тогда, когда
(х1 – х3)(у2 – у3) = (х2 – х3) (у1 – у3).
Так как скорости пешеходов постоянны, то х1(t), у1(t), х2 (t), у2(t), х3(t) и у3(t) – линейные функции от времени t и последнее равенство является квадратным уравнением относительно t, которое может иметь не более двух решений t1 и t2. Это и есть те два возможных момента времени, когда все три пешехода могут оказаться на одной прямой.
8. На координатной плоскости Oхy нарисован график функции y = x2. Потом оси координат стёрли, осталась только парабола. Как при помощи циркуля и линейки восстановить оси координат и единицу длины?
Решение
Докажем следующую лемму.
Лемма. Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы.
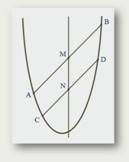
Доказательство. Пусть хорды AB и CD параболы лежат на параллельных прямых
y = kx + a и y = kx + b,
тогда абсциссы точек A, B, C, D – это корни уравнений
x2 = kx + a и x2 = kx + b,
а абсциссы точек M и N – полусуммы корней этих уравнений, то есть по теореме Виета равны k/2. Следовательно, точки M и N лежат на прямой х = k/2, которая параллельна оси Oy. Лемма доказана.
Вернёмся к исходной задаче.
Последовательно осуществляем следующие построения:
1) две параллельные прямые, каждая из которых пересекает параболу в двух точках;
2) прямую через середины получающихся отрезков;
3) перпендикуляр к этой прямой, пересекающий параболу в двух точках А и В;
4) серединный перпендикуляр к отрезку АВ – это ось Оу;
5) ось Ох перпендикулярна Оу в точке пересечения с параболой;
6) единичный отрезок – абсцисса пересечения прямой у = х с параболой.
9. Учитель написал на доске квадратный трехчлен х2 + 10х + 20, после чего по очереди каждый из учеников увеличил или уменьшил на единицу либо коэффициент при х, либо свободный член, но не оба сразу. В результате на доске оказался написан квадратный трехчлен х2 + 20х+10. Верно ли, что в некоторый момент на доске был написан квадратный трехчлен с целыми корнями?
Решение
Первый способ.
Заметим, что при каждом изменении трехчлена его значение в точке х = – 1 изменяется на 1 (в ту или другую сторону). Значение первого трехчлена
f(x) = х2 + 10х + 20
в этой точке равно f(–1) = 11, а последнего,
g(x) = х2 + 20х+10,
— g(–1) = –9. Поэтому в какой-то промежуточный момент на доске был написан трехчлен
h(х) = х2 + pх + q, для которого h(–1)=0. Оба его корня – целые числа: один равен –1, другой по теореме Виета равен –q.
Второй способ.
Каждому квадратному трёхчлену
x2 + bx + c
поставим в соответствие точку координатной плоскости Оbc, где вдоль оси Оb будем откладывать значения второго коэффициента, а вдоль Ос – свободного члена. Многочленам
х2 + 10х + 20 и х2 + 20х +10
будут соответствовать точки
А(10; 20) и В(20; 10),
соответственно. Предложенные в условии операции предполагают перемещение от точки А к точке В вдоль узлов некоторой ломаной L. Узлы L – некоторые целочисленные точки плоскости Оbc, а длина каждого звена L равна 1 (соседние звенья могут лежать на одной прямой).
Так как точки А и В расположены в разных полуплоскостях относительно прямой
с = b – 1,
то ломаная L одним из своих узлов имеет точку этой прямой. Значит, одним из промежуточных многочленов будет многочлен вида
х2 + b0х + (b0 – 1)
с целым b0 и целыми корнями –1 и 1 – b0.
10. Какова вероятность того, что корни квадратного уравнения x2 + 2bx + c = 0 действительны?
Решение
Для того чтобы вопрос задачи имел смысл, предположим, что точка (b; c) равномерно распределена на квадрате с центром в начале координат и стороной 2B. Решим задачу при фиксированном значении B, а затем устремим B к бесконечности, так что b и c могут принимать любые значения.
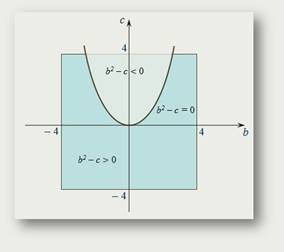
На рисунке более тёмная выделенная область отвечает случаю действительных корней,
более светлая – комплексных.
Для того чтобы уравнение имело действительные корни, необходимо и достаточно, чтобы
b2 - c > 0.
На приведенном рисунке изображена парабола с = b2 и показана область, где наше уравнение имеет действительные корни для B = 4.
Нетрудно подсчитать, что площадь «комплексной» области равна (4 · B3/2)/3 (при B > 1), а площадь всего квадрата, конечно, равна 4B2. Следовательно, вероятность того, что корни комплексные, равна 1/(3√ В). При B = 4 она составляет 1/6. Действительно,
| (4 · B3/2) / 3 | = | = | ||
| 4B2 | 3 · √ В | 3 · √ 4 |
С ростом B значение дроби 1/√ В стремится к нулю, так что вероятность того, что корни вещественные, стремится к 1.
Замечание. Рассмотренная задача отличается от такой же задачи, связанной с уравнением
ax2 + 2bx + c = 0.
Конечно, можно разделить на a, но если a, b и c были независимы и равномерно распределены в некотором кубе, то b/a и c/a уже зависимы и распределены неравномерно.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|