
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Полиномы Лежандра.. Полиномы Лагерра.
Полиномы Лежандра.
Французский математик Адриен Мари Лежандр, помимо того, что он был фанатом Якоби и придумал свои полиномы как частный случай полиномов Якоби, был лучшим другом как всех студентов, так и всех жителей антиутопии системы классических ортогональных полиномов. Всех очень бесило наличие веса-жандарма ρ (х), и Лежандр сделал то, чего хотели все и очень давно: положил его равным тождественным единице.
Как же похорошели классические ортогональные полиномы при Лежандре, стоило только убрать вес!
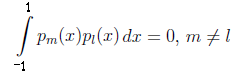
(от -1 до 1 – напомним, что Лежандр фанат Якоби и рассматривал свои полиномы только как частный случай его)
Ну в чистом виде скалярное произведение, без всяких дурацких весов!
Глядя на «якобинскую» формулу
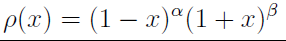
Мы легко скажем, что для этого Лежандр положил
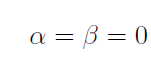
Формула Родрига даёт
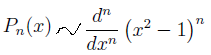
Полиномы Лагерра.

В качестве веса Лагерр выбрал

Обсудим его выбор. У нас интеграл несобственный, от 0 до 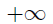 , следовало бы позаботиться о том, чтобы интеграл
, следовало бы позаботиться о том, чтобы интеграл
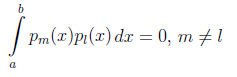
сходился даже для полиномов самых больших степеней. Нужна какая-то быстро затухающая на правом конце функция, затухающая быстрее, чем полином любой степени. На ум как раз сразу приходит е-х. Ну и домножение на произвольную степенную функцию её быстрого убывания не губит.
Надо ещё проверить, что данный вес удовлетворяет уравнению Пирссона, т. е. 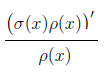 (для многочленов Лагерра это
(для многочленов Лагерра это 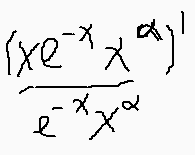 )- линейная функция.
)- линейная функция.
Проверяем и уберждаемся:
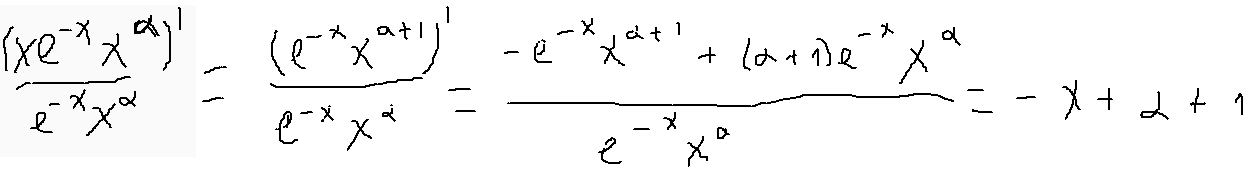
Обозначаются многочлены Лагерра
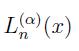
Формула для них:
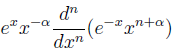
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|