Полиномы Якоби.

Стр 1 из 3Следующая ⇒

Получим всё-таки

формулу Родрига,

которая нам даст явное выражение для нахождения КОПов.

Шаг 1.

Будем плясать от полученного ОУШЛ:

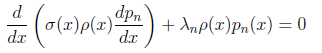
Перепишем с использованием прямой пропорциональности:

Докажем, что для натуральных m< =n

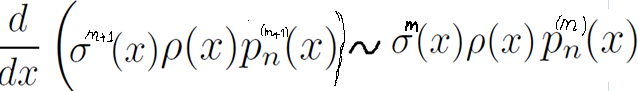
Это легко. Вспомним свойство 3: если мы все многочлены из СКОП продифференцируем, то у нас по прежнему будет СКОП, только вес домножится на σ (х). Если ещё раз продифференцируем – то ещё раз домножится на σ (х)… Продифференцируем m раз – вес будет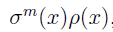

Вот мы как раз и решили продифференцировать m-1 и для полученной СКОП записать ОУШЛ. По сравнению с оригинальным ОУШЛ

Мы исправили р на его m-ю производную, первую производную р на (m+1)-ю, а вес ρ (х) на 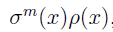. Вот и получили:

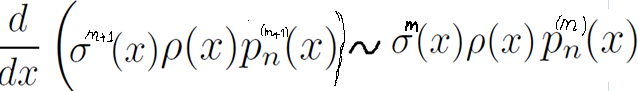
Или, что то же самое:

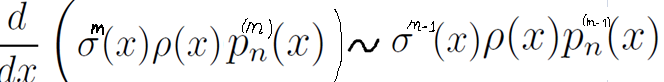
Шаг 2, вариант 1.

Теперь давайте запишем их в ряд, уменьшая m:

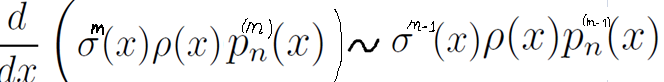
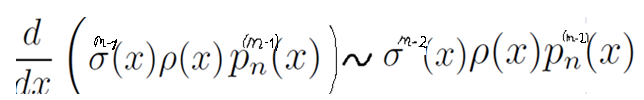
Левая часть каждой прямой пропорциональности – это производная от правой части прямой пропорциональности.

Если мы эту цепочку раскрутим, всё увеличивая и увеличивая порядок производных, до исходного ОУШЛ

то получим

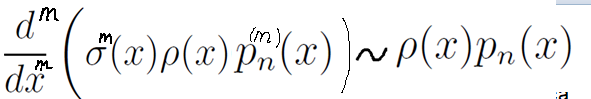
Если вам непонятно, откуда взялась m-тая производная, предложу другое рассуждение.

Шаг 2, вариант 2.

От прямой пропорциональности, полученной в шаге 1

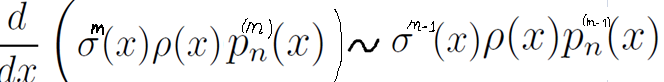
верной для всех m, для обеих частей возьмём (m-1)-тую производную. Учтём, что слева одна производная уже есть, значит, и в итоге там будет m-тая производная.

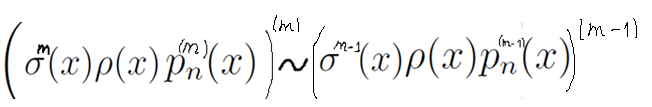
И вот уже теперь уже будем записывать в ряд для разных m:

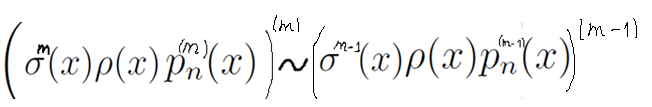
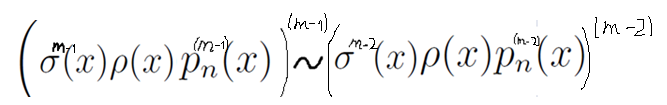
Левая часть каждой прямой пропорциональности – это в точности правая часть предыдущей прямой пропорциональности.

Если мы так раскрутим до исходного ОУШЛ

То и получим

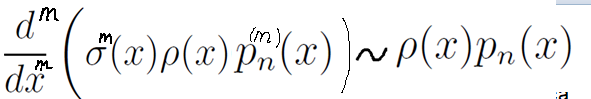
Шаг 3.

Так или иначе получили

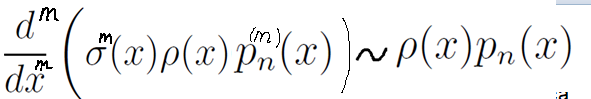
Ура! Дело в том, что n-тая производная р_n(х) константа (не забываем, что р_n – многочлен n-той степени). Эта константа свободно выносится из-под n-ной производной и в конце концов мы её можем отправить в прямую пропорциональность.

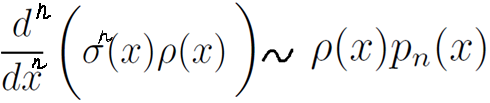
Оооо, а в правой части то, что нам нужно! Почти! Сейчас только на ρ (х) поделим:

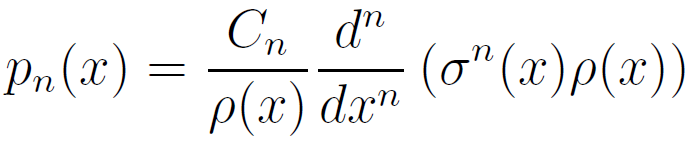
Мы получили формулу Родрига для вычисления классических ортогональных многочленов!

Наличие индекса у коэффициента пропорциональности С говорит нам то, что константа не единая для всех СКОП, а мы вправе выбирать её любой для каждого многочлена.

Замечание: Боголюбов выписывает точные выражения для коэффициентов С_n. И они, если сделать кучу его подстановок, получаются очень сложные. Он там для их поиска считает СЗ ОЗШЛ и вообще дико запаривается.

Это всё делается с одной целью – нормировать полиномы, чтобы их норма была 1. Но ради этого приходится запоминать противные коэффициенты.

На мой взгляд, овчинка выделки не стоит.

Также Боголюбов на лекциях рассказывает производящую функцию. Она нахрен не нужна для понимания темы, но может попасться на экзамене. Поэтому её ботать в течение семестра смысла никакого нет. Я эту тему вынес в отдельную методичку «ММФ к экзамену».

Рассмотрим частные случаи КОПов.

Полиномы Якоби.

Наверное, эта фамилия прежде всего ассоциируется с якобинцами, Великой Французской революции, когда всем рубили головы… Якоби (родившийся, правда, уже в 19-м веке) вот тоже не удержался и решил порубить числовую прямую, установив a=-1, b=1.

(Я знаю, что аналогия тупая, но, как правило, чем тупее аналогия, тем лучше она запоминается. Только из этих соображений).

Т. к. по определению

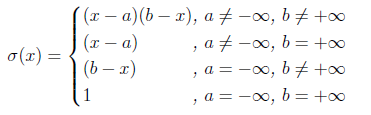
То для полиномов Якоби сразу запишем

Сигма, конечно, это хорошо, но нам гораздо интересней узнать вес. Он, очевидно, будет зависеть от выбора линейной функции.

Оказывается, что в зависимости от выбора линейной функции τ (х)=Ах+B мы получим двухпараметрическое семейство весов:

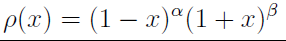
Где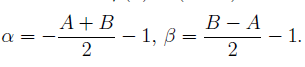

Полиномы Якоби обозначаются БОЛЬШОЙ буквой Р, указывая сверху в скобках выбранные α и β: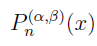

По формуле Родрига с точностью до коэффициента

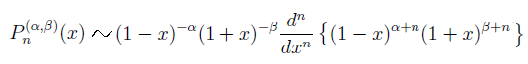
У полиномов Якоби есть три частных случая.

Первые два:

Обозначаются буквами T и U.

Сразу вопрос: а зачем они нужны?! В чём их прикол?!

Ну, нужны они, как сказал Боголюбов, в вычислительной математике. А вот ответить «В чём прикол» я могу и сейчас. Об этом умолчал Боголюбов, но не Википедия! Сейчас расскажу.

Скопируем из Википедии вид полиномов Чебышёва первого рода (недоверчивые Фомы могут проверить, формула для вычисления многочленов Чебышёва у них имеется)

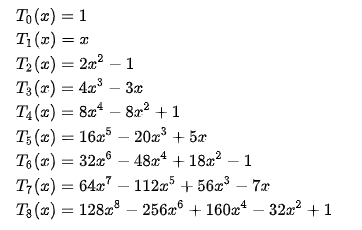
И давайте построим графики:

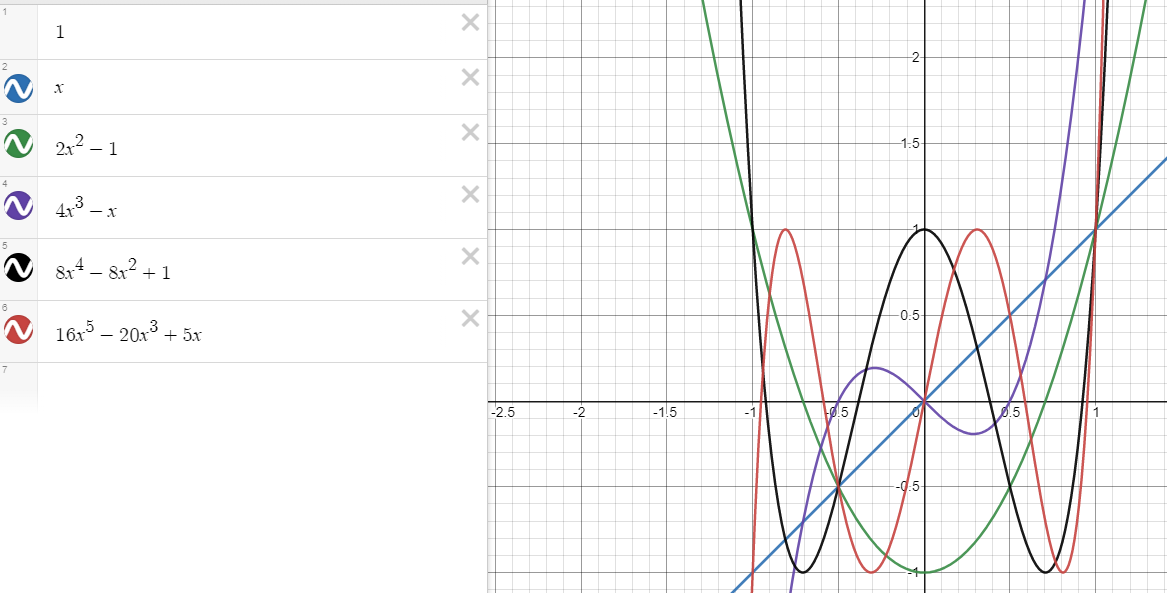
А вот и обещанный прикол: за пределами [-1.. 1] они развлекаются как хотят, а вот внутри [-1.. 1] ютятся в квадрате – их абсолютные значения не превосходят 1!

Случайно ли это? Разумеется, нет. Давайте вернёмся… к школьному курсу тригонометрии.

Вне сомнения, вы помните формулу косинуса двойного угла

cos(2x)=2сos²(х)-1

А если у вас школа была продвинутая, вам могли давать заодно ещё и формулу косинуса тройного угла

сos(3x)=4сos²(х)-3cos(x)

А если у вас не было такой формулы – вот вам вывод:

сos(3x)=cos(2x+x)=cos(2x)cos(x)-sin(x)sin(2x)=

(2сos²(х)-1)*cos(x)-sin(x)*2*sin(x)*cos(x)=

2сos³(х)-cos(x)-2sin²(x)*cos(x)=

2сos³(х)-cos(x)-2(1-cos²(x))*cos(x)=

2сos³(х)-cos(x)-2cos(x)+2cos³(x)=

=4сos²(х)-3cos(x)

Что-то напоминает…

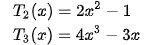
Ну вот неслучайно J Оказывается, что

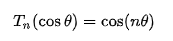
Теперь понятно, почему на [-1.. 1] многочлены Чебышёва ютятся в несчастном квадрате.

Пользуясь этим формулами, можно легко получить и рекуррентную формулу для полиномов Чебышёва:

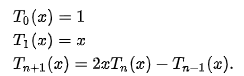
Для многочленов Чебышёва второго рода простую тригонометрическую суть придумать сложно. Но рекуррентная формула есть и для них – причём та же, что и для первого рода, просто U₁ другой, нежели Т₁:

Если что, все эти развлекухи с косинусами Боголюбов не рассказывал и на экзамене не спросит, но вам для справки.

А нам в физике, как обещал Боголюбов, очень пригодится третий частный случай полиномов Якоби -

12 3 Следующая ⇒