• многочлени Лежандра. • символ Лежандра

• многочлени Лежандра

Багаточлени Лежандра - певна ортогональна система многочленів, на відрізку 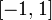по мірі Лебега. Багаточлени Лежандра можуть бути отримані з многочленів 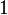, , 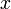, , 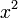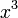і т. д. ортогоналізації Грама - Шмідта. Названі по імені французького математика Адрієн Марі Лежандра.

Можуть бути обчислені за прямими формулами: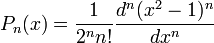

Або по рекурентним: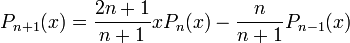

Також вони є рішеннями диференціального рівняння Лежандра: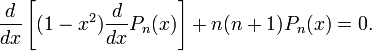

Твірна функція для многочленів Лежандра дорівнює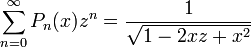

Умова ортогональності цих поліномів на відрізку [-1, 1]:

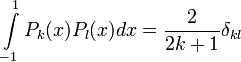
Перші чотири многочлена Лежандра рівні: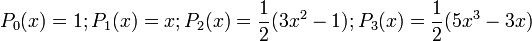

Багаточлени Лежандра (разом з приєднаними функціями Лежандра 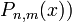природно виникають в теорії потенціалу. Сферичні функції - це функції ( в полярних координатах 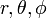виду

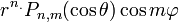и 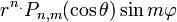, де функції 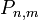- функції Лежандра - задовольняють диференціального рівняння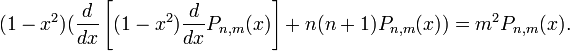

Сферичні функції задовольняють рівняння Лапласа усюди в R3 ( при n < 0 - усюди, крім нуля ) і служать ортогональним базисом для представлення рішень загального вигляду для цього рівняння. Функції Лежандра 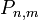( при m = 0 вони збігаються з відповідними многочленами Лежандра ) можуть бути обчислені через многочлени Лежандра за формулами: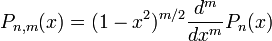

• символ Лежандра

Символ Лежандра - функція, яка використовується в теорії чисел. Введено французьким математиком А. М. Лежандром. Символ Лежандра є окремим випадком символу Якобі, який в свою чергу є окремим випадком символу Кронекера - Якобі.

Нехай a - ціле число, і p - непарне просте число. Символ Лежандра визначається наступним чином:

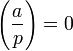§ , якшо 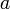ділиться на .

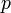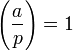§ , якщо 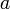є квадратичним вирахуванням за модулем p, тобто існує таке ціле x, що .

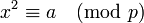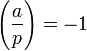§ якщо a є квадратичним невирахуванням по модулю Р

⇐ Предыдущая 123 Следующая ⇒